Рассмотрим пример.
Пусть X(t), ![]() , - скалярный ССП, его
спектральная плотности равна
, - скалярный ССП, его
спектральная плотности равна 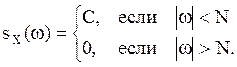 Ковариационная
функция СП X(t) имеет вид
Ковариационная
функция СП X(t) имеет вид 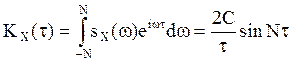 . Чтобы СП X(t)
обладал свойствами белого шума, значение параметра N
должно быть большим, но тогда большой будет и дисперсия
. Чтобы СП X(t)
обладал свойствами белого шума, значение параметра N
должно быть большим, но тогда большой будет и дисперсия ![]() .
.
Чтобы найти предел ![]() при
при ![]() введем
функцию
введем
функцию
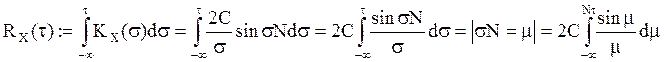 ;
;
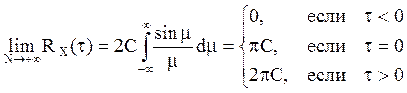 .
Результат следует из равенств
.
Результат следует из равенств 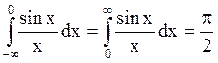 . Если теперь
формально продифференцировать функцию
. Если теперь
формально продифференцировать функцию ![]() по
по ![]() приходим к выражению:
приходим к выражению: ![]() .
.
Отметим еще, что для белого шума справедливо утверждение: сечения белого шума, взятые сколь угодно близко друг к другу, являются некоррелированными с.величинами.
В принципе при
фиксированном N значение коэффициента корреляции сечений ![]() и
и ![]() значимо,
если величина
значимо,
если величина ![]() достаточно мала, так как
достаточно мала, так как 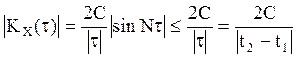 . Поэтому незначимые значения корреляции
будут получаться при достаточно большом значении
. Поэтому незначимые значения корреляции
будут получаться при достаточно большом значении ![]() (см.
(см. ![]() ).
).
Рассмотренный СП X(t), ![]() , является одной из моделей белого шума.
, является одной из моделей белого шума.
В качестве другой
модели белого шума часто используют СП X(t), ![]() , с экспоненциальной ковариационной
функцией
, с экспоненциальной ковариационной
функцией ![]() ,
, ![]() .
.
Для такого процесса 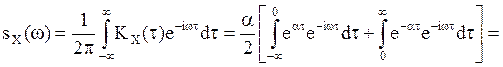
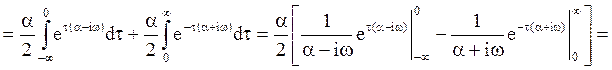
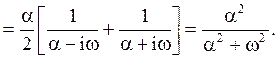 В
этом случае
В
этом случае ![]() и
и ![]() . В
этом процессе сечения его в различные моменты времени – не
коррелированны. Отметим еще в заключение, что термин «белый шум» возник
по двум причинам. Во-первых, из физики известно, что белый свет имеет на всех частотах
одинаковую интенсивность,стационарный белый шум обладает тем же свойством ;
во-вторых, подобные процессы впервые привлекли внимание в радиотехнике, где их
наличие приводит к возникновению шумов в линиях радиопередач.
. В
этом процессе сечения его в различные моменты времени – не
коррелированны. Отметим еще в заключение, что термин «белый шум» возник
по двум причинам. Во-первых, из физики известно, что белый свет имеет на всех частотах
одинаковую интенсивность,стационарный белый шум обладает тем же свойством ;
во-вторых, подобные процессы впервые привлекли внимание в радиотехнике, где их
наличие приводит к возникновению шумов в линиях радиопередач.
4.4. Преобразование стационарного случайного процесса при его прохождении
через линейную динамическую систему
Системы- это совокупность взаимодействующих предметов любой природы. Математической моделью системы называется совокупность четырех элементов: 1) пространства состояний; 2) пространства входных сигналов; 3) пространства выходных сигналов; 4) соотношений, связывающих элементы этих пространств. Система считается заданной , если задана ее математическая модель.
Основной характеристикой модели является оператор системы, связывающий входные и выходные сигналы. Нас будут интересовать только линейные операторы:
![]() , (16)
, (16)
где Х(t)- входной сигнал, Y(t)-выходной сигнал системы.
Стационарной ( однородной) системой называется такая система, у которой при любом сдвиге входного сигнала во времени без изменения его формы, т.е. при замене Х(t) на X(t-h ) при любом h , выходной сигнал претерпевает тот же сдвиг во времени, тоже не изменяя своей формы.
Далее будем рассматривать только такие линейные системы и называть их просто системами.
Входной сигнал X(t)
как непрерывную функцию можно представить разложением на бесконечно малые мгновенные
импульсы X(t)=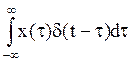 , тогда получаем
выражение для выходного сигнала
, тогда получаем
выражение для выходного сигнала
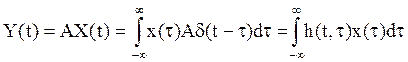 (17)
(17)
Функцию h(t,η) – реакцию системы в момент времени t на единичный мгновенный импульс δ(t-η) в момент времени η называют импульсной переходной функцией системы.
Для стационарных систем h(t,η)= h(t-η).
Основной
характеристикой систем (линейных однородных ) является тот факт, что такая система неограниченно долго
усиливает без изменения его формы действующий входной сигнал, представляющий собой
экспоненту ![]() .
Воспользуемся формулой (17) :
.
Воспользуемся формулой (17) :
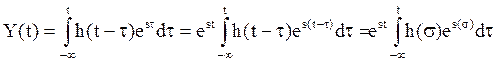 .
Функцию
.
Функцию
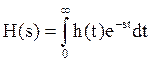 (18)
(18)
называют передаточной функцией (линейной однородной) системы. Поскольку функции
H и h связывает преобразование Лапласа, при этом функция H(s)- функция комплексного переменного s, регулярная в полуплоскости b = Res > α, где α – показатель роста функции
h(t) , то обратное преобразование Лапласа имеет вид
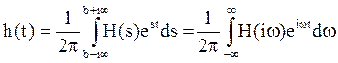 (19)
(19)
Перепишем равенство
(17) для стационарной системы : 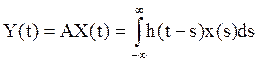 .
.
Умножим обе части полученного
равенства на ![]() и проинтегриркуем по t:
и проинтегриркуем по t: 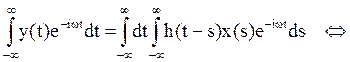
![]()
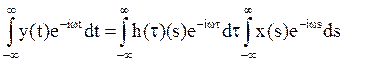
![]() (после замены t-s на τ ). Приняв во внимание
равенство (18) получаем
(после замены t-s на τ ). Приняв во внимание
равенство (18) получаем
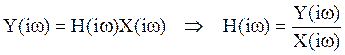 (20)
(20)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.