Стационарные случайные функции

        IY. Стационарные случайные функции

Определение стационарных СП  было дано в параграфе 2.1.  Отметим некоторые свойства таких процессов. Будем полагать их действительными.

        4.1. Свойства стационарных случайных процессов (ССП)

1.  - ковариационная матрица ССП  X(t) (дисперсия в случае скалярного ССП) постоянна.

2. .

Это свойство вытекает из первого свойства моментов 2 порядка (см. главу 1). Если X(t) – скалярный ССП, то  - ковариационная функция является четной.

3.  - ковариационная функция скалярного ССП не может быть больше ее значения в начале координат.

4. 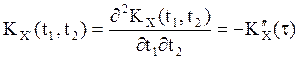, , -  производная ССП также является ССП . В частности, ,     , поскольку в точке  функция  имеет максимум. Это означает, что значение любого  ССП  и ее первой производной в одной и той же точке не коррелированны!

Везде далее мы будем рассматривать СП  X(t),  стационарные в широком смысле.

        4.2. Некоторые типовые ковариационные функции

1.  - экспоненциальная ковариационная функция;

2.  - экспоненциально-косинусная ковариационная функция;

3. ,  .

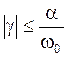Эти три функции – основные, они порождают ковариационные функции ССП, то есть все другие ковариационные функции являются линейными комбинациями этих трех.

Графики всех трех функций в точке  имеют угловую точку, следовательно, процессы с такими ковариационными функциями не являются с.к. дифференцируемыми. Исключение составляет третья функция – при 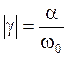  в точке  не имеет угловой точки.

        4.3.   Спектральная теория стационарных случайных функций

По своей сути – это применение идей и методов гармонического анализа к случайным функциям. Гармонический анализ решает задачу представления функции в виде суммы гармоник , каждая из которых соответствует определенной частоте . Множество этих частот образует спектр функции. Зная спектр функции, ее можно восстановить с любой наперед заданной точностью.

При изучении случайных  процессов приходится считаться с тем фактом, что ни одна из реализаций СП не может быть известна заранее. Однако оказывается возможным заранее установить, как распределяются дисперсии СП по частотам составляющих его гармоник.

Такая информация по значимости не уступает знанию спектра детерминированных (неслучайных) функций.

Использование этой информации при изучении СП представляет сущность спектральной теории.

        4.3.1. Стационарные случайные функции с дискретным спектром

Основной задачей является представление скалярного ССП X(t) в виде конечной или бесконечной суммы гармоник  со случайными амплитудами А и фазами  и различными частотами , то есть представление СП  X(t) в виде:

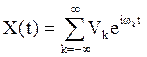                                                               (1)

Здесь - последовательность частот, - последовательность с.в.

Будем полагать, что ,   ковариационная функция процесса  непрерывна и зависит от . Для того, чтобы эти условия  сохранялись при представлении СП в виде (1) необходимо и достаточно, чтобы с. величины , k=1,2,…, были некоррелированными и имели нулевое математическое ожидание:

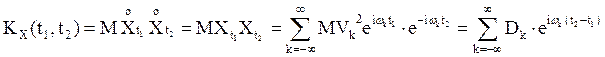  или

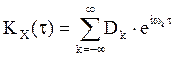,                                                           (2)

где   - дисперсия  с. величин  . Отсюда

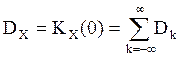                                                           (3)

и дисперсия процесса конечна тогда и только тогда, когда ряд (3) сходится.  При этом  ряд (2) сходится к функции  равномерно (признак Вейерштрасса).

Формула (3)  определяет распределение  дисперсии процесса по частотам его спектра  ,.

В общем случае о представлении ССП Х(t) рядом (1) больше ничего нельзя сказать. Но вот если все частоты ССП  кратны основной частоте , соответствующей некоторому периоду : 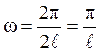, то формула (2) представляет собой ряд Фурье для функции . В этом случае сама формула может быть уточнена. Так, в силу четности  сумму (2) можно переписать в виде:

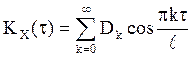                                                          (4)

и 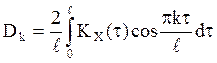  - коэффициенты ряда Фурье.

В силу непрерывности  при  любых   существуют интегралы:

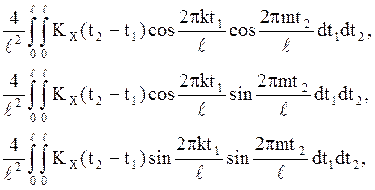
поэтому  процесс X(t)  с.к. интегрируем с весами 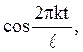 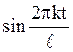, k=1,2,…Следовательно, на множестве Т определен скалярный СП

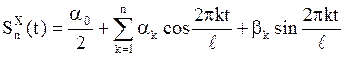                                         (5)

и  , ,  ,  .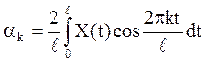

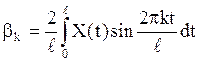Если процесс  является стационарным и с.к. сходится  к исходному процессу X(t), , то можно говорить о спектре частот 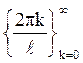 стационарного СП X(t).

Последний вывод является корректным, так как справедлива

        Теорема 1. Если  - ковариационная функция скалярного СП X(t), , с , является непрерывной на отрезке , представима на нем равномерно сходящимся к ней рядом Фурье 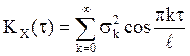  , то

1.  СП , определяемый формулой (5) , является стационарным;

2.  Процесс    с.к. сходится к исходному процессу X(t).

        Доказательство.   Из условия, что , следует: , .

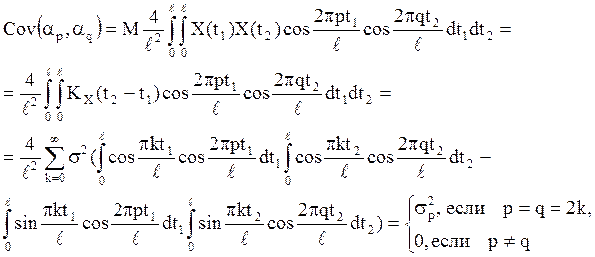
Точно также доказываются равенства:   .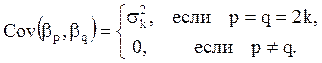

Далее, покажем, что существует с.к. предел  при : , .

.

;

.

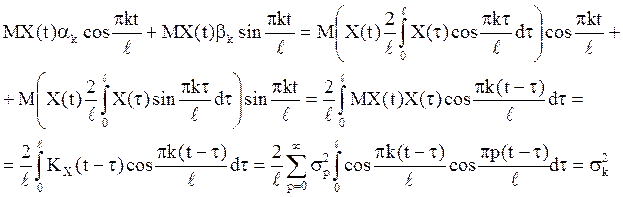
Аналогично, .           Следовательно, 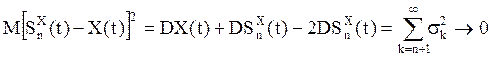  при  как остаток сходящегося ряда.

Замечание. В результате получаем, что дисперсии с.величин  являются коэффициентами ряда Фурье для ковариационной функции исходного СП X(t) при соответствующих частотах, то есть 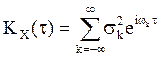, и .

Пример 16.   Пусть X(t), , - стационарный скалярный СП с нулевым математическим ожиданием и ковариационной функцие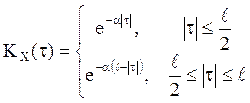й   и  - известная константа. Убедимся в том , что процесс X(t) представим рядом Фурье.