Стационарные случайные функции, страница 3

Далее, из интегрируемости функции  следует возможность представления ее интегралом Фурье: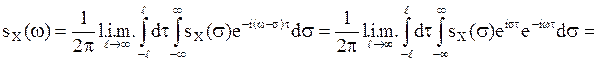

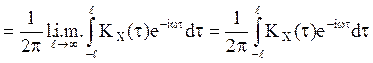, если - абсолютно интегрируема – получили равенство (9).

Поскольку интеграл (8) равномерно сходящийся, функция    непрерывная, тогда СП X(t) – с.к. непрерывен.

Равенство (7) называют  спектральным разложением ССП  X(t).  Из формул (11), (9) следует, что функции  и  характеризуют распределение дисперсии ССП  X(t) по его спектру частот ,  поэтому функцию  называют спектральной функцией, а  - спектральной плотностью ССП X(t).Можно считать  аналогом  в непрерывном случае последовательности дисперсий {D_k} некоррелированных случайных амплитуд гармоник, составляющих ССП X(t).

Если  не содержит -функций, СП X(t) можно считать составленным из некоррелированных гармонических колебаний всех частот  с бесконечно малыми случайными амплитудами , дисперсии которых равны приближенно ( точное равенство :).СП в этом случае называют СП с непрерывным спектром.

Если   содержит -функции , то СП называют СП с непрерывно-дискретным спектром.

В заключение заметим, что на основании формул (9) и (10) за характеристику СП зачастую принимают не ковариационную функцию , а спектральную плотность , что особенно удобно при применении частотных методов исследования стационарных систем.

        4.3.3. Свойства спектральной плотности

Если  считать СП X(t) – скалярным   вещественным, то:

1. .

Это свойство очевидно, если вспомнить, что мы говорили о  в предыдущем параграфе в пояснении к формуле (11).

2. .

Если  СП – векторный вещественный, то ,  если X(t) – комплексный  ССП , то .

.

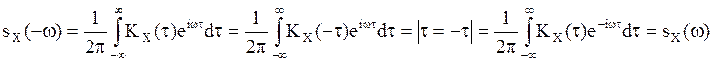3. .

Результат следует из выражения для : .

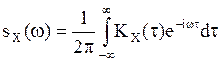4. .

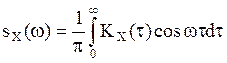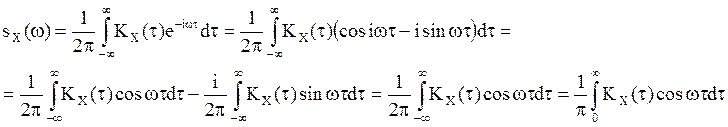
в силу четности подынтегральной функции по .

5. .

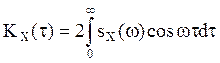6..

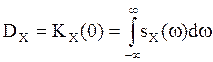Замечание. Если СП  X(t) – векторный , то спектральная плотность  представляет из себя матрицу, диагональные элементы которой – спектральные плотности компонент вектора , недиагональные элементы - так называемые спектральные взаимные плотности компонент и вектора X(t). На основании  полученного свойства 2 спектральной плотности в случае векторного процесса  для  взаимных спектральных плотностей действительного процесса справедливы формулы: , .

        4.3.4. Спектральное разложение

        Теорема .  Любой  с.к. непрерывный  ССП  X(t) может быть представлен спектральным разложением 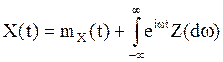 , а его  ковариационная функция и спектральная плотность связаны соотношениями (9) и (10).

Эту теорему мы не сможем доказать, не выходя за рамки математического аппарата, применяемого в теории СП.

Формула ( 9)  впервые была получена Н. Винером и Н. Хинчиным, поэтому формулы (9) и (10) называют формулами Винера-Хинчина.   Формула (12) была впервые получена           Г. Крамером и А.Н. Колмогоровым.

        4.3.5. Стационарный белый шум

Белый шум можно определить как слабую с.к. производную СПНРП. Любой СПНП, имеющий дифференцируемую ковариационную функцию, является и СПНРП, следовательно, имеет слабую с.к. производную, называемую белым шумом в строгом смысле. Это только обобщенные с. функции. . Если же рассматривать слабые с.к. производные СПНРП, но с зависимыми приращениями, то получаются обычные с. функции.

Пусть V(t) – белый шум постоянной интенсивности , то есть  . Такой белый шум называется стационарным белым шумом. Для стационарного белого шума 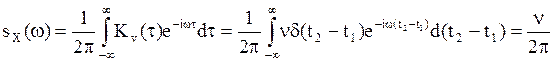                        (13)

Итак, 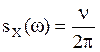                                                                                                 (14) 

Мы уже говорили, что белый шум физически не осуществим. Но из физических соображений ясно, что любая динамическая система является инерционной и очень высокие частоты не могут оказывать значимого влияния на ее поведение. Это открывает возможность моделирования с помощью реальных СП белого шума, например, имеющего  постоянную (или почти постоянную) спектральную плотность в определенной полосе частот, пренебрегая поведением спектральной плотности вне этой полосы.