На рис 4.10 приведены четыре семейства кривых, пользуясь которыми можно определить число пар зацепления и передаточные числа для них при минимальном моменте инерции зубчатой передачи, приведенной к валу двигателя. Эти кривые охватывают диапазон чисел от 1,0 до 1000. Например, если общее передаточное число равно 75, то по кривым рис 4.10 находим число пар равное 5, приближенные передаточные числа для которых при минимуме инерции находятся на кривых рис. 4.11 (i1=1,55; i2=1,7; i3=2,0; i4=2,8; i5=5,2)
Эти значения уточняются, чтобы попасть в ряд нормальных передач и максимально приблизиться к общему передаточному числу.
В целях упрощения или экономии на практике число ступеней обычно принимают меньшим, чем получатся по кривым на рис.4.10 для данного общего передаточного числа i. В этом случае номограмма на рис.4.12 является полезным вспомогательным средством, т.к. она дает передаточные числа ступеней при минимальном моменте инерции для любого количества выбранных ступеней. Особенно удобно пользоваться этой номограммой совместно с кривыми на рис. 4.10.
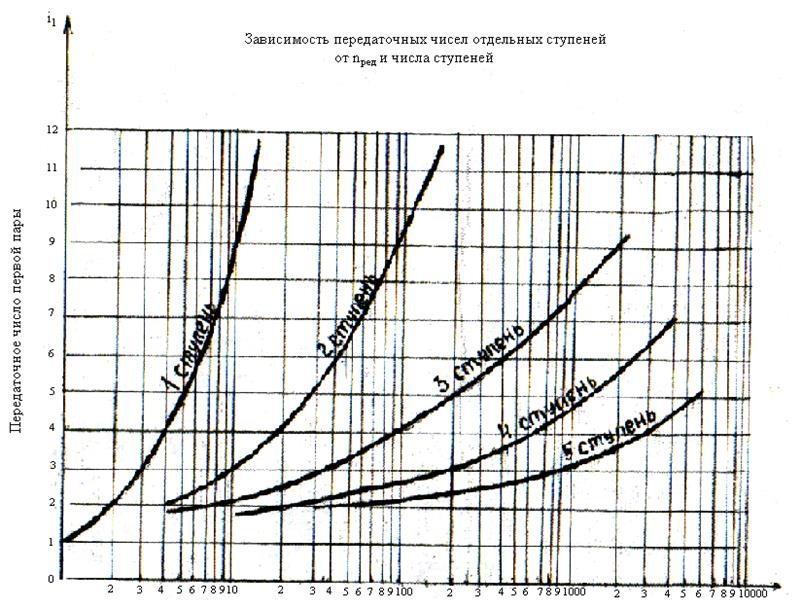
Рис. 4.10

Рис. 4.12
Так для i=75 на рис 4.10 находим n=5. В целях упрощения конструкции места можно принять n=4.
Тогда, обращаясь к номограмме, накладываем линейку на точку 4, выражающую количество ступеней, и устанавливаем ее так, чтобы она проходила через общее передаточное число 75 на правой вертикальной шкале. На левой вертикальной шкале линейка укажет, что передаточное число первой ступени должно быть 1,72 (вместо 1,55 для пяти ступеней согласно показаниям кривой рис.4.11). Округляя его до 1,75, находи остающееся передаточное число; разделив 75 на 1,75, получаем приближенно 43. Повторяя операцию находим передаточное число второй ступени, исходя из трех ступеней и общего передаточного числа 43, аналогичным образом находим передаточные числа остальных ступеней. Для проверки возрастания инерции при выборе четырех ступеней вместо пяти обратимся к кривым на рис.4.10. Отношение момента инерции зубчатой передачи к моменту инерции первой ведущей шестерни при n=5 составляет 6,2, а при n=4 – 7,1.
В силовых передачах и в передачах, работающих с ударами, в которых условия прочности играют важную роль, размеры шестерен приходится увеличивать в той части передачи, где передаваемые скорости низки, а моменты велики. Обычно число зубцов на ведущих шестернях остается постоянным с минимумом, зависящим от угла зацепления и профиля зуба. Моменты инерции валов, подшипников принимаются пропорциональными моментам шестерен и суммируются с ними.
Одним из способов выбора ширины зуба и диаметра начальной окружности ведущей шестерни в любом зацеплении является соблюдение отношения:
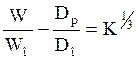 ,
(4.37)
,
(4.37)
где W – ширина зубца в зацеплении;
Dp – диаметр начальной окружности ведущей шестерни;
К – передаточное число от двигателя к данной ведущей шестерне.
Индекс «О» - отношения к ведущей шестерне двигателя.
Другое эмпирическое соотношение, учитывающее увеличение нагрузки на колеса, имеет вид:
![]() (4.38)
(4.38)
Соотношения 4.37 и 4.38 показывают необходимость увеличения ширины зубцов и диаметра колес с ростом нагрузки.
Момент инерции J шестерни, как диска, пропорционален ширине колес и четвертой степени диаметра. Минимизируя приведенный момент инерции передачи с учетом неодинаковой ширины зубцов и соотношений 4.37 и 4.38 можно построить кривые для выбора оптимального числа пер и передаточных чисел из условия минимума приведенного момента инерции и учета возрастания нагрузки в зацеплении. Графики приведены на рис. 4.13. Из графиков следует, что для малых передаточных чисел и малого числа ступеней результаты, получаемые из кривых рис.4.13 и 4.11 мало отличаются друг от друга. Для больших i и n уширение колес дает возможность уменьшить приведенный момент инерции почти в два раза.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.