Помимо рассмотренных режимов работы двигателя, возможен выбор рабочих точек на характеристиках, соответствующих точкам (Рис. 4.6). Передаточные числа редуктора в случае выбора этих рабочих точек будут равны, соответственно:
; 
; 
; 
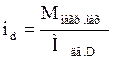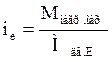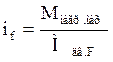
При работе в указанных режимах двигатель развивает момент на валу нагрузки равный моменту сил сопротивления. Однако, в силу того, что мощность, развиваемая двигателем в режимах «C,D,E,F» больше мощности, требуемой нагрузкой, то скорость вращения вала нагрузки будет больше wнагр. Это приемлемо, т.к. не ухудшает точности системы, а наоборот, повышает ее добротность по скорости.
Таким образом, в режимах «C,D,E,F» двигатель сообщает нагрузке мощность, больше требуемой, что проявляется во вращении вала нагрузки с большей скоростью.
Как следует из вышеуказанного, передаточное число редуктора в случае Рдв.ном>Рнагр.мах не определяется однозначно. Оно может быть выбрано любым в пределах:
(4.19)
Выбор i является поиском разумного компромисса между увеличением статической ошибки системы и уменьшением люфтов при i® iв, и уменьшением статической ошибки с увеличением люфтов при i®ia. Что касается добротности системы в скорости, то она выше в режимах «C,D,E,F».
Выбор i по изложенной методике возможен в случае наличия характеристик Рдв=¦(Мвр) или возможности их построения. При отсутствии таковых, передаточное число редуктора выбирается из следующего соотношения:
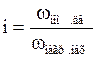(4.20)
В этом случае момент нагрузки, приведенный к валу двигателя, будет находиться в пределах:
МА<Мпр<Мном (4.21)
и двигатель будет иметь хороший запас по скорости. Помимо перечисленных факторов при окончательном выборе передаточного числа редуктора необходимо учитывать инерционность нагрузки и связанную с ней постоянную времени системы «двигатель – редуктор – нагрузка», которая определяется выражением:
,
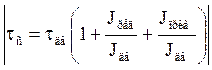(4.22)
где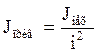 
Очевидно, что для повышения быстродействия системы (уменьшения tс) необходимо уменьшать Jприв (посредством увеличения i), имея при этом в виду, что i должно лежать в пределах iв£ i £ ia и момент инерции редуктора также влияет на величину tс.
Графический метод нахождения оптимального передаточного числа
В условиях необычной нагрузки или нелинейной характеристики двигателя оптимальное передаточное число может быть найдено графическим методом.
Мощность нагрузки может быть определена как:
Рмех = wмех (J Емех + М'см), (4.23)
где J = Jмех + i2Jдв, М'см= Мсм + i Мтр.дв (4.24)
Тогда Рмех=wмех[(Jмех+i2Jдв)Емех+(Мсм+i Мтр.дв)], т.к. в расчет введены приведенные значения моментов двигателя, то общая требуемая мощность является функцией передаточного числа. Необходимо выяснить, может ли двигатель развить указанную выше мощность РМЕХ и одновременно определить оптимальное передаточное число.
Для ряда значений i двигатель, работающий при скорости iwмех будет приводить в действие нагрузку со скоростью wмех. Момент двигателя Мдв, соответствующий скорости wмех (wдв=iwмех), может быть определен из механической характеристики выбранного двигателя. Тогда мощность двигателя будет:
Рдв=1,025wдвМдв (4.25)
wдв [об/мин] = iwмех
Мдв [кГм]
Рдв [Вт]
Если кривые мощности двигателя Рдв и мощности нагрузки Рмех совместить на одном графике как функции передаточного числа, то достаточность мощность двигателя для приведения в действие нагрузки станет очевидной. Одновременно выявится область возможных передаточных чисел. Описанный порядок расчета не учитывает влияния инерции зубчатых передач, которое может быть значительным. Если силы инерции необходимо учесть, то сначала определяют i = i0 из рисунка. Затем определяют число ступеней передачи и производят расчет редуктора. Определяют эквивалентный момент редуктора, отнесенный к валу нагрузки. Тогда уравнение 4.24 примет вид:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.