Механические передачи следящих систем, страница 5

Р_мех=w_мех[(J_мех+J_ред+i²J_дв)Е_мех+(М_см + i М_тр)]                         (4.26)           

Пользуясь уравнением 4.26, наносят вторую кривую Р_мех на график и определяют новое передаточное число. Почти для всех систем этого расчета бывает достаточно, хотя в случае необходимости расчет может быть повторен с новым i₀.

Выбор числа ступеней передач и передаточных чисел для них

Эффективный момент зубчатой передачи для заданного общего передаточного числа может быть снижен надлежащим распределением передаточного числа между отдельными ступенями. Так как момент инерции шестерен пропорционален четвертой степени диаметра:  , то первые одну или две ступени выбирают с зубчатыми колесами малого диаметра и относительно малым передаточным числом. Последующие ступени оказывают малое влияние на J_ред. Для большинства зубчатых передач в следящих системах удовлетворительные результаты могут быть получены при выборе на всех ступенях ведущих колес одного диаметра с одинаковой шириной зуба и из одного материала. Инерцией валов, подшипников и других мелких деталей обычно пренебрегают. Однако для крупных систем необходим учет и этих деталей.

Рассмотрим схему двухступенчатого редуктора. Задача заключается в выборе передаточных чисел i₁ и i₂, которые снижают до минимума момент инерции передачи, приведенный к валу двигателя (рис. 4.9).

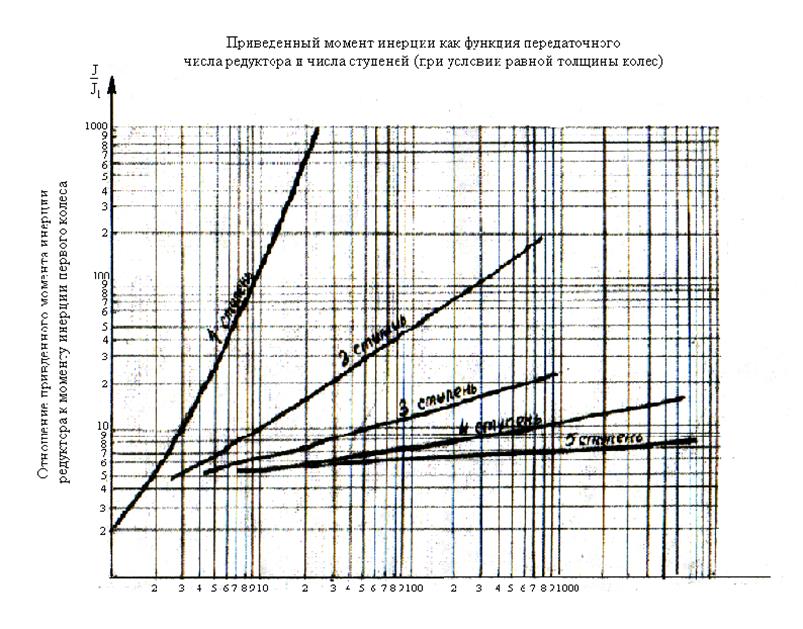
Рис 4.9

Общий момент инерции четырех колес, отнесенный к валу двигателя, может быть выражен, как:

                   (4.27)

Т.к. D₁ = D₃, то 4.27 можно записать так:

       (4.28)

Где J₁ – момент инерции 1 и 3 колеса.

Подставляя в уравнение 4.28 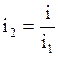, получим

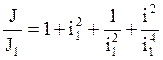                                                 (4.29)

Дифференцируя уравнение 4.29 по i₁, будем иметь

                                            (4.30)

Полагая,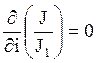

Получим:

i₁⁶ – i₁² – 2i² = 0                                                    (4.31)

Подставляя в уравнение 4.31 i = i₁i₂, будем иметь

                                                        (4.32)

Или, если 1 пренебрежимо мало по сравнению с i₁⁴, то

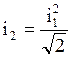                                                            (4.33)

Уравнение 4.1 дает распределение общего передаточного числа между двумя парами редуктора. В многоступенчатой зубчатой передаче с минимальной инерцией каждая пара смежных зубчатых сцеплений должна иметь минимальную инерцию. Поэтому каждая пара (за исключением ближайшей у двигателя) связана с предыдущей отношением 4.32. Отсюда, применяя это уравнение последовательно в 2,3 и более раз для различных значений i₁, можно вычислить минимальный коэффициент инерции для передачи с тремя, четырьмя и более парами.

По уравнению 4.31 можно определить приближенное передаточное отношение первой пары, минимизирующее приведенный момент инерции:

                                                          (4.34)

По первому передаточному числу рассчитываем отношение момента инерции зубчатой передачи к моменту инерции ведущей шестерни на валу двигателя, пользуясь уравнениями 4.29 и 4.34.

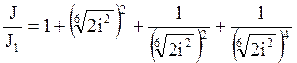                                 (4.35)

Для сравнения приведем отношение всего момента инерции к моменту инерции шестерни на валу двигателя, для одноступенчатой передачи с тем же передаточным числом i:

                                                         (4.36)           

При i=10 уравнения 4.35 и 4.36 дают относительный момент инерции всей передачи для одноступенчатой B»10 раз больше, чем для двухступенчатой.

Таким образом, введение многоступенчатой передачи существенно снижает момент инерции передачи. Однако необходимо учитывать и другие обстоятельства, связанные с ограничением габаритов, условиями изготовления, стоимостью и т.д.

И так, описанный выше анализ может быть распространен на значительное количество ступеней передачи. Результаты оформляются в виде удобных для пользования кривых и номограмм, позволяющих выбирать оптимальное число ступеней передачи для данного общего передаточного числа и получать отношение при оптимальном распределении по ступеням передаточного числа. Например, для общего передаточного числа 10 кривые дают оптимальное число ступеней 4 и отношение приведенного момента инерции зубчатой передачи к моменту инерции зубчатой шестерни равное 5.