

Корреляционная функция одномерного случайного процесса Kx(t1,t2) характеризует взаимную зависимость его значений, соответствующих различным моментам времени, и формально определяется через двумерную ПРВ:
![]()
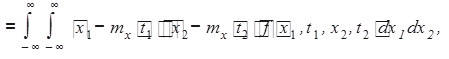 (8.3)
(8.3)
причем при t1= t2= t имеем
Kx(t,t)= Dx(t). (8.4)
Большая корреляция – хорошо.
В частном случае стационарного случайного процесса:
mx(t)=mx=const, Dx(t)=Dx=const, а корреляционная функция становится функцией одного аргумента:
Kx(t1,t2)=Kx(t2– t1)=Kx(τ), τ=t2– t1, Kx(0)=Dx.
Смысл соотношений (8.1)-(8.3) состоит в определении характеристик случайного процесса усреднением по множеству реализаций.
Если стационарный случайный процесс обладает свойством эргодичности (среднее по множеству реализаций совпадает со средним по времени), перечисленные его характеристики могут быть найдены всего по одной реализации и без использования плотности распределения:
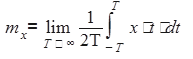 ,
(8.5)
,
(8.5)
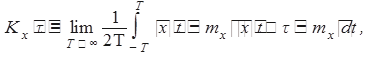 (8.6)
(8.6)
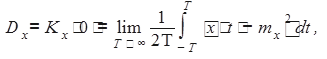 (8.7)
(8.7)
где x(t) - детерминированная реализация случайного процесса X(t). Соотношения (8.5)-(8.7), очевидно, более удобны для практики.
Для стационарного случайного процесса вводится также весьма удобная для построения расчетного аппарата функция спектральной плотности
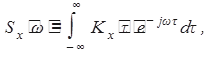 (8.8)
(8.8)
характеризующая распределение мощности, или интенсивности, случайных колебаний X(t) по различным частотам. Соответственно имеют место соотношения:
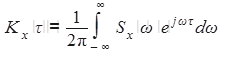 ,
,
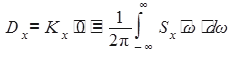 .
(8.9)
.
(8.9)
Таким образом, для одномерного случайного процесса X(t) вместо многомерной ПРВ используются две группы характеристик, описывающих его с двух взаимно дополняющих точек зрения:
- с точки зрения распределения значений X(t) в конкретный момент времени (f(x,t), mx(t), Dx(t)...);
- с точки зрения зависимости значений X(t) в разные моменты времени (Kx(t1, t2) или Kx(τ),Sx(ω) для стационарного процесса).
Связь между этими двумя группами характеристик сводится только к формальному совпадению значений дисперсии, определяемых по (8.2) и через Kx(τ) или Sx(ω).
Отметим важный для ряда практических задач частный случай - белый шум (может обладать любым з-ном распределения). Корреляционная функция (представляет собой дельта-функцию) белого шума имеет вид:
Kx(t1,t2)
= G(t1)δ(t1-t2), где G(![]() ) -
интенсивность белого шума.
) -
интенсивность белого шума.
Для стационарного белого шума G(t)=G=const и может быть определена спектральная плотность:
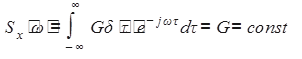 .
.
При построении модели системы в пространстве состояний приходится рассматривать многомерный случайный процесс X(t)=(X1(t),X2(t),...,Xn(t)), составляющими которого являются случайные фазовые переменные системы.
Распределение мгновенных значений такого процесса для определенного момента времени t описывается одномерной ФРВ
Fx(x1,x2,…xn)=P(X1<x1,X2<x2,…,Xn<xn)
или ПРВ
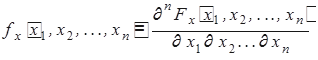
векторной случайной величины X=(X1,X2,...,Xn). На практике обычно ограничиваются использованием только моментов распределения первого и второго порядка.
Средние значения фазовых переменных
описываются их математическими ожиданиями ![]() .
.
Взаимная зависимость значений фазовых переменных описывается матрицей корреляционных функций:
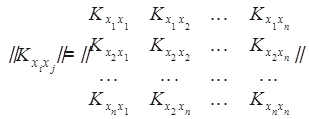 . (8.10)
. (8.10)
Главную диагональ матрицы (8.10) образуют
корреляционные функции фазовых переменных (автокорреляционные функции) ![]() , определяемые по (8.3). Остальные элементы
(i≠j) - взаимные корреляционные функции фазовых переменных:
, определяемые по (8.3). Остальные элементы
(i≠j) - взаимные корреляционные функции фазовых переменных:
![]()
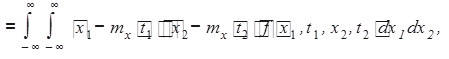 (8.11)
(8.11)
где f(x1,t1,x2,t2)- совместная ПРВ значений процесса X1, наблюдаемых в момент времени t1, и значений процесса X2, наблюдаемых в момент времени t2.
При t1=t2=t матрица (8.10) превращается в матрицу корреляционных моментов связи, или матрицу моментов:
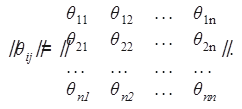 (8.12)
(8.12)
Диагональные элементы матрицы (8.12) представляют собой дисперсии фазовых переменных
![]() .
.
Остальные элементы - ковариации
![]() , то есть матрица (8.12) симметричная.
, то есть матрица (8.12) симметричная.
Совокупность случайных входных воздействий системы также рассматривается как векторный случайный процесс G(t)=(G1(t),G2(t),...,Gn(t)), для которого используются аналогичные характеристики.
Если все входные сигналы - белые шумы,
элементы матрицы (8.10) имеют вид ![]() и вместо (8.12)
задается матрица интенсивностей
и вместо (8.12)
задается матрица интенсивностей
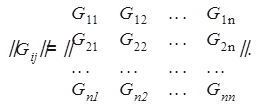 (8.13)
(8.13)
где Gii=Gi - интенсивности составляющих входного сигнала
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.