Лекция 20. Анализ устойчивости и качества импульсных систем
Если представить дискретную передаточную функцию замкнутой импульсной системы в форме
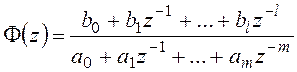 , (20.1)
, (20.1)
можно перейти к разностному уравнению, связывающему входной и выходной сигналы системы. При этом для дискретных передаточных функций сохраняется свойство: знаменатель, определяющий вид левой части разностного уравнения, для всех передаточных функций конкретной системы одинаков. Его называют характеристическим полиномом замкнутой системы:
![]() или
или ![]() .
.
 Асимптотическая устойчивость
системы определяется корнями характеристического полинома. В соответствии с
(18.9) для устойчивости дискретной или импульсной системы необходимо и
достаточно, чтобы все корни zi, i=1,2,…,m характеристического
полинома удовлетворяли условию:
Асимптотическая устойчивость
системы определяется корнями характеристического полинома. В соответствии с
(18.9) для устойчивости дискретной или импульсной системы необходимо и
достаточно, чтобы все корни zi, i=1,2,…,m характеристического
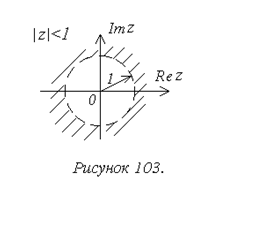
полинома удовлетворяли условию: ![]() . Область
устойчивости на комплексной плоскости будет иметь вид круга единичного радиуса
(рисунок 103). Таким образом, проверка устойчивости может быть выполнена, если
будет выполнена достаточно трудоемкая процедура вычисления корней уравнения D(z)=0.
. Область
устойчивости на комплексной плоскости будет иметь вид круга единичного радиуса
(рисунок 103). Таким образом, проверка устойчивости может быть выполнена, если
будет выполнена достаточно трудоемкая процедура вычисления корней уравнения D(z)=0.
Известно, что для непрерывных систем существует удобный математический аппарат анализа устойчивости и качества замкнутой системы, не требующий вычисления корней характеристического полинома. Возможность использования этого математического аппарата для импульсных систем обеспечивается на основе дополнительного w-преобразования дискретной передаточной функции. Преобразование выполняется на основе подстановки
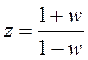 , (20.2)
, (20.2)
где w -новая комплексная переменная.
После подстановки (20.2) в (20.1) будет получена новая дискретная передаточная функция замкнутой системы
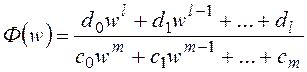 (20.3)
(20.3)
с характеристическим полиномом
![]() . (20.4)
. (20.4)
Определим требование к корням полинома (20.4) для обеспечения устойчивости системы. Оно может быть получено на основе неравенства
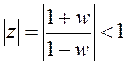 или
или ![]() .
.
С
учетом записи w=a+jb получим ![]() .
Очевидно, это неравенство может быть выполнено только при a<0.
.
Очевидно, это неравенство может быть выполнено только при a<0.
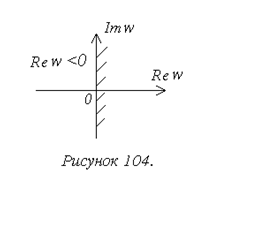 Таким образом, область
устойчивости для корней характеристического полинома D(w)
импульсной системы совпадает с областью устойчивости для корней
характеристического полинома D(p) непрерывной системы (рисунок 104).
Поэтому после перехода к передаточной функции (20.3) на импульсную систему
может быть распространен весь математический аппарат исследования устойчивости
непрерывных систем.
Таким образом, область
устойчивости для корней характеристического полинома D(w)
импульсной системы совпадает с областью устойчивости для корней
характеристического полинома D(p) непрерывной системы (рисунок 104).
Поэтому после перехода к передаточной функции (20.3) на импульсную систему
может быть распространен весь математический аппарат исследования устойчивости
непрерывных систем.
Необходимое условие устойчивости: все коэффициенты характеристического полинома должны быть одного знака. Для систем с характеристическим полиномом первого или второго порядка это условие является необходимым и достаточным.
Для систем с характеристическим полиномом более высокого порядка при выполнении необходимого условия для обеспечения устойчивости требуется выполнение какого-либо достаточного условия (критерия устойчивости).
Критерий Гурвица и другие алгебраические критерии могут быть использованы для полинома D(w) непосредственно.
Для использования частотных критериев устойчивости и методов анализа качества в случае импульсных систем необходимы дополнительные преобразования.
После естественной замены в передаточных функциях s=jw, где w - частота входного гармонического сигнала, получим:
![]() ,
, 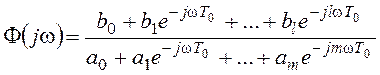 .
.
Такие передаточные функции неудобны для дальнейших аналитических преобразований. Поэтому для импульсных систем вместо реальной частоты используется псевдочастота, переход к которой производится на основе w-преобразования.
Следствием (20.2) является соотношение:
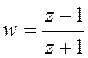 .
.
Выполнив подстановку ![]() ,
получим:
,
получим:
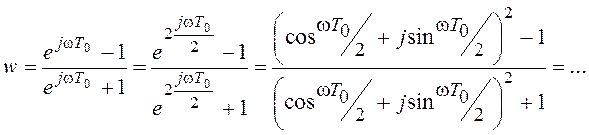
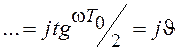 , где
величина
, где
величина 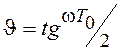 называется относительной псевдочастотой.
Удобнее использовать абсолютную псевдочастоту
называется относительной псевдочастотой.
Удобнее использовать абсолютную псевдочастоту
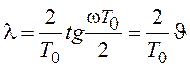 , (20.5)
, (20.5)
так
как на малых частотах 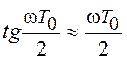 и
и ![]() , то есть совпадает с реальной частотой
гармонического сигнала.
, то есть совпадает с реальной частотой
гармонического сигнала.
Частотный критерий устойчивости Найквиста и связанные с ним методы анализа качества и синтеза систем применяются для импульсных систем с использованием псевдочастотных характеристик, получаемых из передаточной функции разомкнутой системы W(z) путем подстановок (20.2) и вытекающей из (20.5)
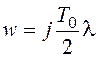 .
(20.6)
.
(20.6)
При этом нужно иметь в виду, что изменению абсолютной
псевдочастоты в пределах ![]() согласно (20.5)
соответствует изменение реальной частоты в пределах
согласно (20.5)
соответствует изменение реальной частоты в пределах 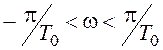 .
При дальнейшем увеличении w будет проявляться периодичность
зависимости (20.5). Поэтому результаты, получаемые на основе псевдочастотных
характеристик, следует считать достаточно точными для
.
При дальнейшем увеличении w будет проявляться периодичность
зависимости (20.5). Поэтому результаты, получаемые на основе псевдочастотных
характеристик, следует считать достаточно точными для 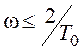 ,
или
,
или 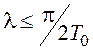 , а анализ более высоких псевдочастот
позволяет делать только качественные выводы.
, а анализ более высоких псевдочастот
позволяет делать только качественные выводы.
Точность системы в установившемся режиме может быть оценена на основе теоремы о конечном значении.
Установившаяся ошибка от задающего воздействия:
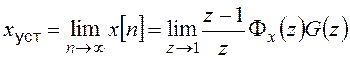 .
.
Установившаяся ошибка от возмущающего воздействия:
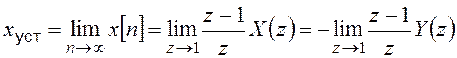 , где
Y(z) находится в соответствии с (19.9).
, где
Y(z) находится в соответствии с (19.9).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.