Лекция 22. Управляемость и наблюдаемость линейных систем
Понятия управляемости и наблюдаемости входят в число основных в современной теории управления. Смысл понятия управляемости состоит в возможности приведения системы в любое требуемое состояние, а наблюдаемости – в возможности определения состояния системы по результатам измерения выходных сигналов.
Состояние X(1) является достижимым из состояния X(0), если существует допустимое управление u(t) на интервале tÎ[t0,t1], t1<<∞ такое, что система под его воздействием переходит из X(0)=X(t0) в X(1)=X(t1).
Система называется сильносвязанной, или вполне достижимой, если у нее каждое состояние достижимо из любого другого.
Пример 1.
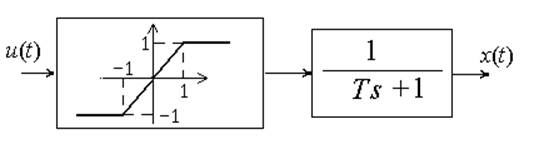
Система на
рисунке не обладает таким свойством, так как, например, из любого состояния
![]() ее невозможно перевести в какое либо
состояние из области
ее невозможно перевести в какое либо
состояние из области ![]() .
.
Для линейных систем понятие сильносвязанности переходит в понятие полной управляемости.
Рассмотрим линейную систему:
![]() ,
,
![]() , где X=(x1,x2,…xn) – вектор
переменных состояния, U=(u1,u2,…ur) – вектор
входных сигналов (вектор управления), Y=(y1,y2,…yl) – вектор
выходных сигналов, A – квадратная
матрица размерностью
, где X=(x1,x2,…xn) – вектор
переменных состояния, U=(u1,u2,…ur) – вектор
входных сигналов (вектор управления), Y=(y1,y2,…yl) – вектор
выходных сигналов, A – квадратная
матрица размерностью ![]() , B – матрица входов размерностью
, B – матрица входов размерностью
![]() , C– матрица выходов
размерностью
, C– матрица выходов
размерностью ![]() .
.
Система называется полностью управляемой, если для любых начального момента времени t0³0 и конечного состояния X(1)=X(t1) существуют t1³t0 и ограниченное по величине управление U(t) на интервале tÎ[t0,t1] такое, что из заданного начального состояния X(0)=X(t0) достигается X(1).
Если система стационарна, можно принять t0=0, совместить X(0) с началом координат фазового пространства и говорить о существовании конечного управления, переводящего систему в любую заданную точку фазового пространства за конечный интервал времени.
Как следует из определения, свойство управляемости не связано с выходными сигналами и, следовательно, не зависит от матрицы C.
Критерий управляемости: матрица управляемости U=[B|AB|…|An-1B] не вырождена, то есть detU¹0.
Система называется нормальной (нормализуемой), если управляемость имеет место по каждой компоненте вектора управления.
Для систем со скалярным управлением свойства управляемости и нормализуемости совпадают.
Далее при рассмотрении примеров ограничимся такими системами.
Пример 1. Модель системы имеет вид:
![]() ,
,
![]() ,
,
y=x1.
Составим матрицы A и B:
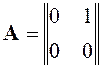 ,
, 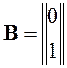
и найдем матрицу управляемости:
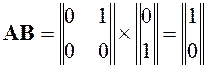 ,
,
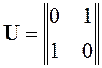 .
.
 Получим detU=-1. Следовательно,
данная система полностью управляема.
Получим detU=-1. Следовательно,
данная система полностью управляема.
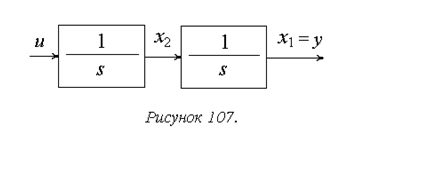
Это нетрудно видеть и по ее структурно-динамической схеме, показанной на рисунке 107.
Пример 2. Модель системы задана в векторно-матричной форме:
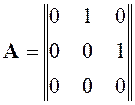 ,
, 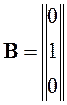 .
.
Найдем матрицу управляемости:
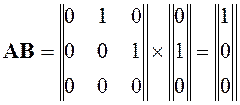 ,
,
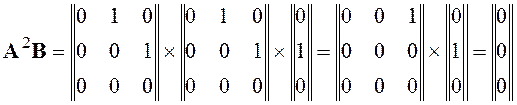 ,
,
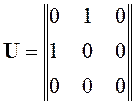 .
.
Получим detU=0. Следовательно, данная система не является полностью управляемой.
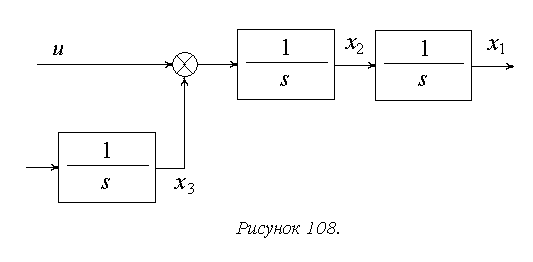
Действительно, по ее структурно-динамической схеме, показанной на рисунке 108, видно, что управляющий сигнал не влияет на фазовую переменную x3.
Пример 3. Модель системы задана структурно-динамической схемой (рисунок 109).
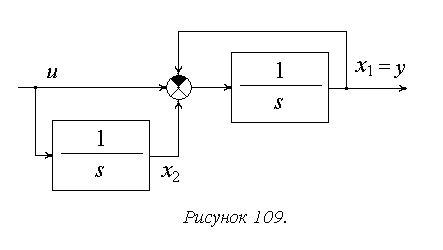
Составим дифференциальные уравнения системы:
![]() ,
,
![]() ,
,
y=x1.
Составим матрицы A и B:
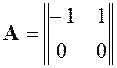 ,
, 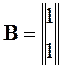
и найдем матрицу управляемости:
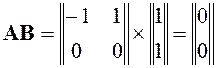 ,
,
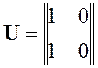 .
.
Получим detU=0. Система не является полностью управляемой. Отметим, что в данном случае по структурно-динамической схеме это не очевидно. Причина отсутствия полной управляемости для данной системы состоит в том, что ее передаточная функция содержит сократимые элементы (нуль и полюс, совпадающие по величине):
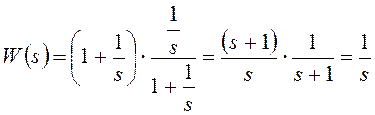
Такую передаточную функцию называют вырожденной.
Система называется полностью наблюдаемой, если для любого начального момента времени t0³0 существует такое t1³t0, что вектору выходных сигналов Y(t) на интервале tÎ[t0,t1], полученному для известного на том же интервале вектора управления U(t), соответствует единственное значение X(0)=X(t0).
Если система линейна и стационарна, можно принять t0=0 и U(t)=0 и говорить о единственности решения задачи нахождения X(0)=X(0) по известному на интервале времени [0,t1] вектору Y(t).
Как следует из вышесказанного, свойство наблюдаемости для линейных систем не связано с управлением U и, следовательно, не зависит от вектора B.
Критерий наблюдаемости: матрица наблюдаемости
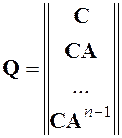
не вырождена, то есть detQ¹0.
Вернемся к примеру 1. Составим матрицу наблюдаемости:
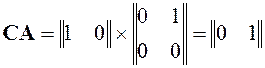 ,
,
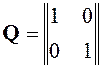 .
.
Получим detQ=1. Система полностью наблюдаема.
Пример 4. Модель системы имеет вид:
![]() ,
,
![]() ,
,
![]() ,
,
y=x1.
Составим матрицы A и C:
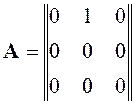 ,
, ![]() .
.
Найдем матрицу наблюдаемости:
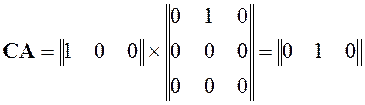 ,
,
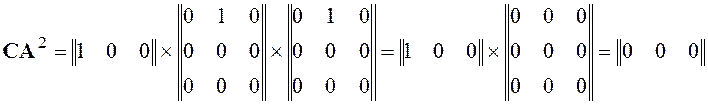 ,
,
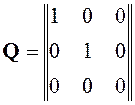 .
.
Получим detQ=0. Следовательно, данная система не является полностью наблюдаемой.
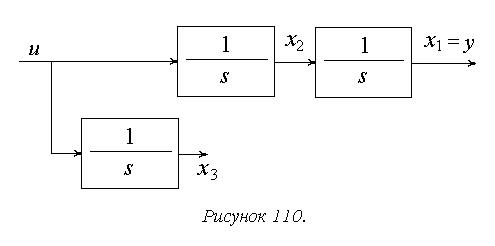
Тот же вывод нетрудно сделать и по структурно-динамической схеме системы (рисунок 110), где видно, что фазовая переменная x3 не влияет на выходной сигнал. Следовательно, выходной сигнал не содержит информации об этой фазовой переменной.
Пример 5. Модель системы имеет вид:
![]() ,
,
![]() ,
,
y=x2.
Составим матрицы A и C:
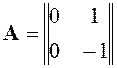 ,
, ![]()
и матрицу наблюдаемости:
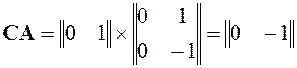 ,
,
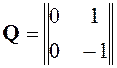 .
.
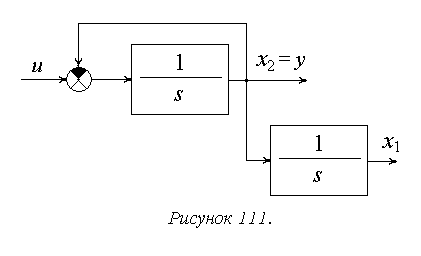
Получим detQ=0. Система не является полностью наблюдаемой. Это достаточно хорошо видно и по структурно-динамической схеме (рисунок 111).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.