Определение типа особой точки и вида фазовых траекторий

Лекция 13.Особые точки и фазовые портреты нелинейных систем.

Обратимся к модели нелинейной системы второго порядка (11.3):

,

.

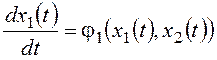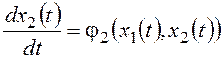Для нахождения особых точек, соответствующих возможным состояниям равновесия системы, производные в левых частях принимаются равными нулю, что приводит к системе нелинейных алгебраических уравнений:

,

.                                            (13.1)

Система (13.1) может иметь одно или несколько решений, определяющих координаты особых точек.

Классификация найденных особых точек выполняется на основе линеаризации модели (11.3). Линеаризация выполняется в окрестности каждой особой точки и основана на использовании разложения нелинейных функций в правых частях (11.3) в ряд Тейлора с последующим сохранением только линейных членов разложения.

В основе линеаризации лежит допущение о том, что в исследуемом динамическом процессе переменные x₁ и x₂, характеризующие состояние системы, являются непрерывными функциями времени и отклоняются от установившихся значений  достаточно мало. Предполагается также, что j₁ и j₂ - непрерывные и дифференцируемые по всем аргументам функции.

Обозначим отклонения фазовых переменных Dx₁, Dx₂. Тогда в динамическом процессе будем иметь:

,  ,  ,  .              (13.2)

Разложение нелинейных функций из правой части (11.3) в ряд Тейлора имеет вид:

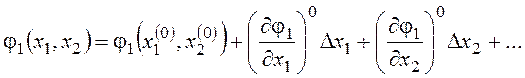
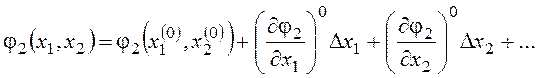,           (13.3)

где 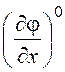- значения частных производных по фазовым переменным в точке разложения. Членами ряда второго и более высокого порядка пренебрегают.

После подстановки (13.2) и (13.3) в исходные уравнения (11.3) и вычитания из полученных уравнений (13.1) получим систему уравнений для отклонений:

,

-

,

---------------------------------------------------------------------------

;

.

-

,

---------------------------------------------------------------------------

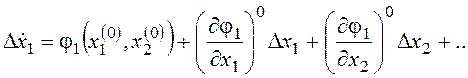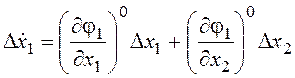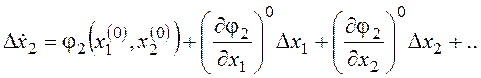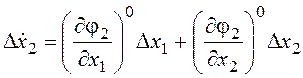, которую используют, отбрасывая обозначения приращений:

,

,

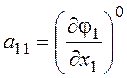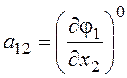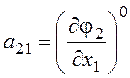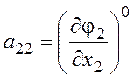,  ,  ,  .       (13.4)

Система уравнений линеаризована в малых окрестностях особых точек, причем ее коэффициенты зависят от координат особых точек.

Теперь определение типа особой точки и вида фазовых траекторий в ее окрестности производится на основе вычисления собственных чисел матрицы А системы (13.4) с использованием всех результатов, полученных ранее для линейных систем.

Полное построение фазового портрета на основе модели (11.3) может быть обеспечено только на основе решения нелинейной системы уравнений численными методами.