Практическое занятие 8. Анализ особых точек и построение фазовых портретов нелинейных систем.
Пример 1.
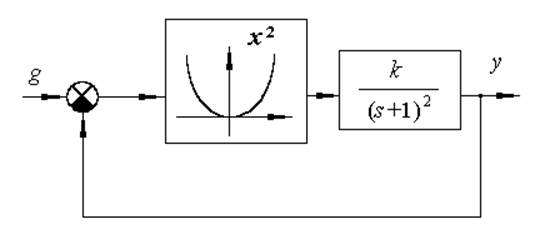
Исходные данные: k=2; g(t)=1(t).
Найти и классифицировать особые точки на фазовой плоскости. Построить примерный фазовый портрет системы.
Запишем общее дифференциальное уравнение системы:
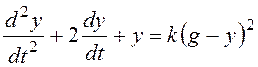
или
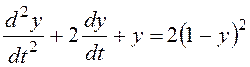
Введем фазовые переменные x1=y, ![]() и перейдем
к модели в форме системы дифференциальных уравнений:
и перейдем
к модели в форме системы дифференциальных уравнений:
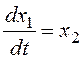 ,
,
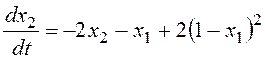 .
.
Рассчитаем координаты особых точек (у нелинейной системы возможны две и более особых точек):
![]() ,
,
![]() ,
,
![]() ,
,
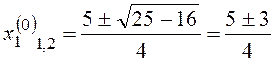 .
.
Найдены две особые точки с координатами (2; 0) и (0,5; 0).
Выполним в общем виде линеаризацию нелинейного уравнения модели:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
,
![]()
-
![]()
-----------------------------------------------------------------------------
![]() .
.
Окончательно линеаризованная модель принимает вид:
![]() ,
,
![]() .
.
Как можно видеть, один из коэффициентов модели зависит от координаты особой точки, что и определяет возможное различие типов особых точек.
Рассмотрим особую точку (2; 0):
![]() ,
,
![]() ;
;
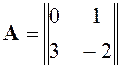 ,
,
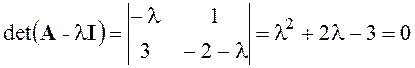 ,
,
l1=-3, l2=1.
Рассмотренная особая точка – седло, фазовые траектории в ее окрестности – гиперболы. В рассматриваемом базисе собственные числа матрицы А определяют наклоны особых линий (асимптот гипербол) x2=(x1-2) и x2=–3(x1-2). Направление движения изображающей точки по фазовым траекториям также определяется рассматриваемым базисом.
Рассмотрим особую точку (0,5; 0):
![]() ,
,
![]() ;
;
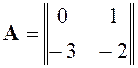 ,
,
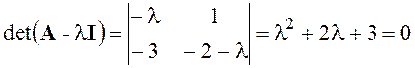 ,
,
![]() .
.
Рассмотренная особая точка – устойчивый фокус, фазовые траектории в ее окрестности – сходящиеся в особую точку спирали. Направление движения изображающей точки по фазовым траекториям – по часовой стрелке.
Результаты проведенного анализа графически отображены на рисунке.
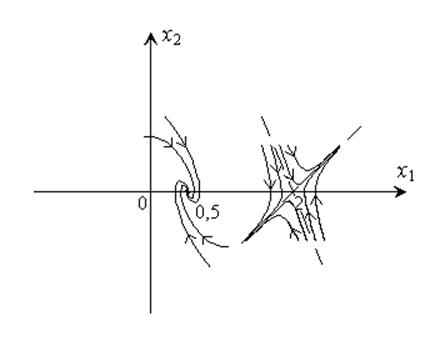
Полный фазовый портрет представлен ниже.
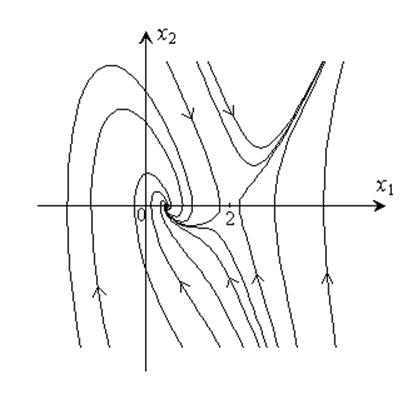
Пример 2.
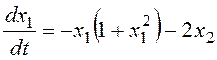 ,
,
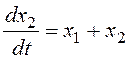 .
.
Найти и классифицировать особые точки на фазовой плоскости. Построить примерный фазовый портрет системы.
Рассчитаем координаты особых точек (у нелинейной системы возможны две и более особых точек):
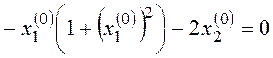 ,
,
![]() ;
;
![]() ,
,
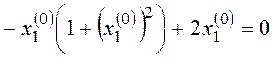 ,
,
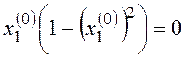 .
.
Найдены три особые точки с координатами (0; 0), (1; -1) и (-1; 1).
Выполним в общем виде линеаризацию нелинейного уравнения модели:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
,
![]()
-
![]()
-----------------------------------------------------------------------------
![]() .
.
Окончательно линеаризованная модель принимает вид:
![]() ,
,
![]() .
.
Рассмотрим особую точку (0; 0):
![]() ,
,
![]() .
.
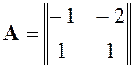 ,
,
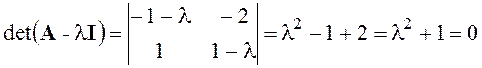 ,
,
![]() .
.
Рассмотренная особая точка – центр, фазовые траектории в ее окрестности – эллипсы.
Для определения направления движения по фазовым траекториям в окрестности точки (0; 0) найдем значения составляющих вектора скорости движения, например, в точке (0,1; 0):
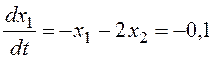 ,
,
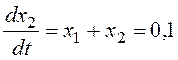 .
.
Движение по фазовым траекториям вокруг центра – против часовой стрелки.
Рассмотрим особую точку (1; -1):
![]() ,
,
![]() .
.
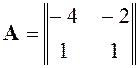 ,
,
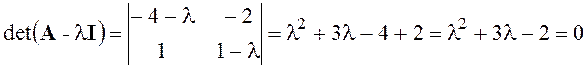 ,
,
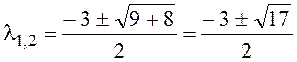 ,
,
l1=-5,62, l2=0,56.
Рассмотренная особая точка – седло, фазовые траектории в ее окрестности – гиперболы. Особые линии – асимптоты гипербол. Их наклоны найдем из уравнения
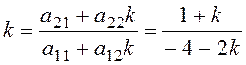
или
![]() ,
,
– 2k2 – 5k– 1 = 0,
2k2 + 5k+ 1 = 0,
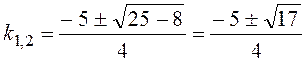 ,
,
k1= –2,28; k2= –0,22.
Для определения направления движения по фазовым траекториям найдем составляющие вектора скорости движения в точке (1,2; –1):
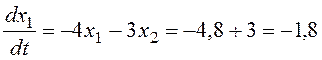 ,
,
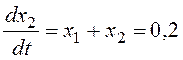 .
.
Вектор скорости в рассмотренной точке направлен влево и вверх.
Обратившись к линеаризованному уравнению
![]() , нетрудно
убедиться, что для особой точки (-1; 1) будут получены
идентичные результаты.
, нетрудно
убедиться, что для особой точки (-1; 1) будут получены
идентичные результаты.
Результаты проведенного анализа графически отображены на рисунке.
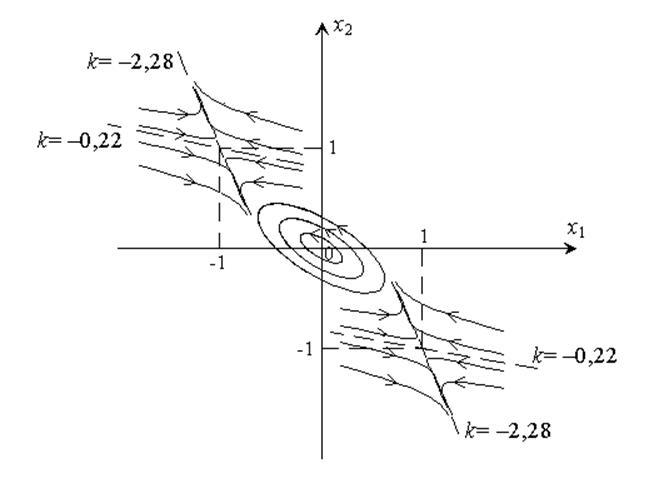
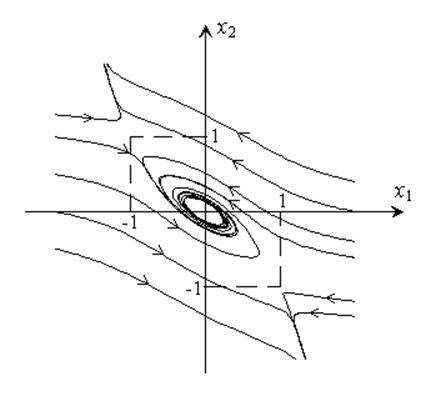
Полный фазовый портрет представлен ниже.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.