Статистическая линеаризация нелинейной стационарной системы

Лекция 10.Статистическая линеаризация нелинейной стационарной системы

Если система включает в себя хотя бы одно нелинейное звено, задача анализа протекающих в ней процессов существенно усложняется. Для нелинейных систем не выполняется принцип суперпозиции. Нелинейное звено вносит существенные искажения в закон распределения преобразуемого сигнала. Тем не менее, возможность использования достаточно простых методов анализа случайных процессов, разработанных для линейных систем, удается здесь обеспечить на основе статистической линеаризации системы.

Статистической линеаризацией называется построение линейной модели нелинейного звена системы управления с учетом характеристик преобразования случайного сигнала линейной частью системы.

Метод статистической линеаризации основан на допущении о наличии у линейной части системы свойства фильтра. Ранее свойство фильтра рассматривалось применительно к преобразованию динамическим звеном или системой периодического сигнала. При преобразовании же случайного сигнала свойство фильтра проявляется иначе и состоит в том, что линейное динамическое звено за счет своей инерционности «нормализует» закон распределения преобразуемого сигнала. Другими словами, независимо от вида закона распределения входного сигнала, выходной сигнал линейной части системы имеет закон распределения, близкий к нормальному. Приближенное условие наличия свойства фильтра сохраняется: степень многочлена R(s) в числителе передаточной функции линейной части должна быть меньше степени многочлена Q(s) в знаменателе.

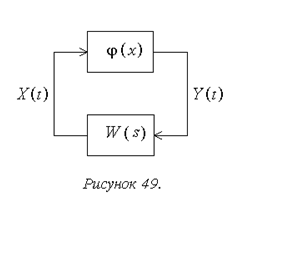Сигнал на входе нелинейного звена, то есть на выходе линейной части (рис. 49), рассматривается в форме , причем благодаря тому, что для него рассматривается нормальный закон распределения, для описания центрированной составляющей ограничиваются дисперсией D_x или среднеквадратическим отклонением σ_x.

Статистическая линеаризация проводится для стационарных процессов или для фиксированных значений m_x и σ_x нестационарного случайного процесса, соответствующих некоторому рассматриваемому  моменту времени.

Если статическая характеристика нелинейного звена j(x) однозначна и дифференцируема по крайней мере для отрезка [m_x-3σ_x; m_x+3σ_x] и s_xдостаточно мала, выполняется прямая линеаризация нелинейности в окрестности  m_x (рис. 50). В этом случае сигнал на выходе нелинейного звена рассматривается в форме:

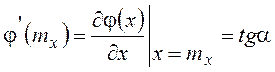,  ,         (10.1)

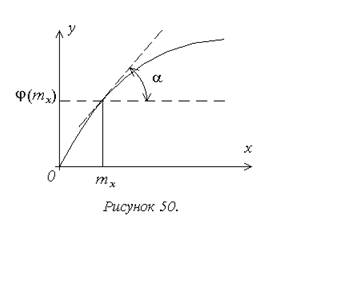где j(m_x) и j'(m_x) - коэффициенты линеаризованной модели нелинейного звена, нелинейно зависящие от m_x; a - угол наклона касательной к функции j(x)  в точкеm_x. Получаемая приближенная зависимость (10.1) оказывается линейной относительно  центрированной составляющей входного сигнала , что равноценно замене  исходной  нелинейной статической характеристики звена касательной в точке, соответствующейm_x.

Для нелинейного звена с несколькими входами статическая характеристика приводится к виду j(x₁,x₂,…,x_n). При выполнении для всех входных сигналов x_i указанных выше условий прямая линеаризация