Анализ и синтез релейной системы методом фазовой плоскости

Лекция 15.Анализ и синтез релейной системы методом фазовой плоскости (продолжение)

Учтем дополнительно к зоне нечувствительности и запаздыванию инерционность устройства управления включением-выключением двигателей. Для этого модель нужно дополнить соответствующим дифференциальным уравнением апериодического звена первого порядка (рисунок 70):

,

,

,

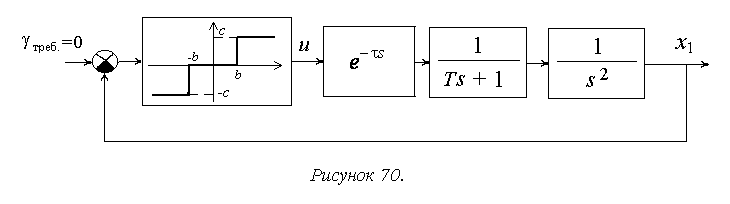
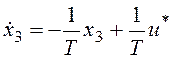u^*(t)=u(t-t),

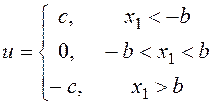                                         (14.6)

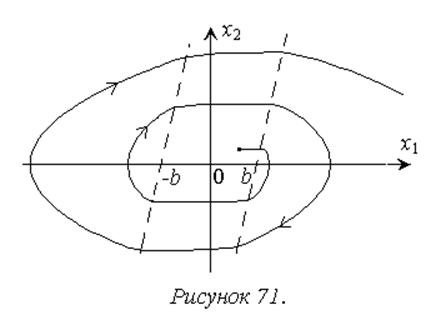
Фазовая траектория с учетом зоны нечувствительности, запаздывания и инерционности показана на рисунке 71. Из рисунка видно, что система остается неустойчивой, причем скорость увеличения амплитуды колебаний возрастает, то есть система удаляется от границы устойчивости.

Как известно из теории линейных систем управления, на устойчивость положительно влияет учет в законе управления производной выходного сигнала. Ограничимся сначала учетом зоны нечувствительности и введем в закон управления для рассматриваемой системы производную (рисунок 72):

,

,

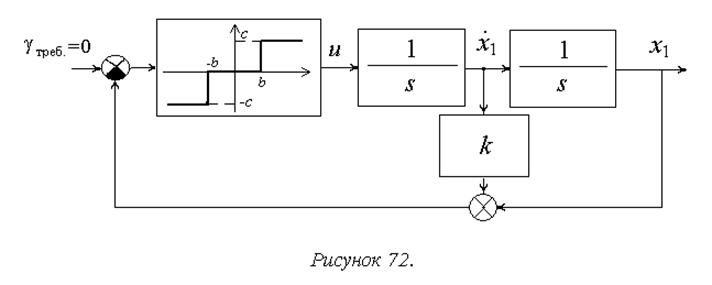
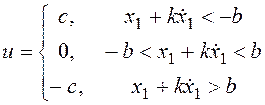                                      (14.7)

Условия смены значений сигнала управления в (14.7) определяют уравнения линий переключения как прямых с отрицательным наклоном:

,

.

В результате получаем сходящиеся фазовые траектории, то есть обеспечивается устойчивость системы (рисунок 73). За счет зоны нечувствительности в рассматриваемой системе имеет место не единственное состояние равновесия, а множество состояний равновесия, отображаемое на фазовой плоскости в рассматриваемых координатах отрезком горизонтальной оси [-b; b]. Процессы, вызванные отклонениями фазовых переменных от состояния равновесия, завершаются в крайних точках этого отрезка.

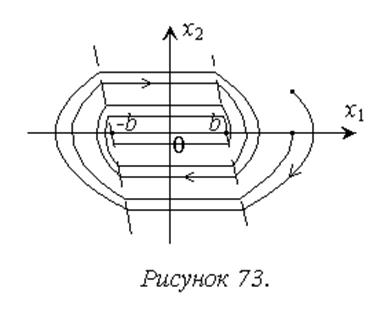
Нетрудно убедиться, что система становится устойчивой при любом k>0, а при наличии в системе запаздывания величиной t при условии k>t.

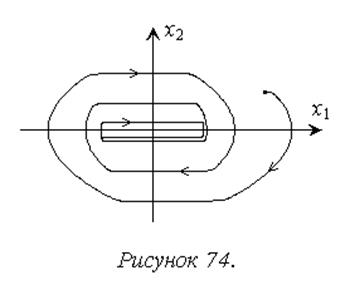
Дальнейшим увеличением k можно обеспечить устойчивость системы и при наличии инерционности. Пример фазовой траектории показан на рисунке 74.

Особенностью систем управления космическими летательными аппаратами является ограниченный и во многих случая невосполнимый ресурс работы двигателей. С этой точки зрения к процессам их функционирования предъявляется дополнительное требование минимизации суммарного интервала времени, когда двигатели включены (u=±c). В ряде случаев в интересах выполнения этого требования принимают допустимыми автоколебания с малой амплитудой. Управление, соответствующее таким требованиям, обеспечивается на основе логического закона управления. Один из простейших вариантов логического закона выглядит следующим образом:

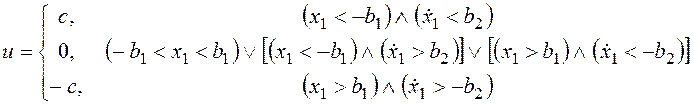
Положение соответствующих ему линий переключения на фазовой плоскости показано на рисунке 75.

Для иллюстрации основных соображений, положенных в основу логического закона управления рассмотрим сначала идеализированный вариант модели системы стабилизации без учета запаздывания и инерционности. Фазовый портрет, представленный на рисунке 76, показывает, что в системе обеспечивается незатухающий колебательный процесс с ограниченной амплитудой. При начальных условиях вне предельного цикла, определяемого величинами b₁ и b₂, колебания сходятся к этому предельному циклу. При начальных условиях внутри указанного предельного цикла параметры установившихся колебаний определяются величиной b₁ и начальными условиями.

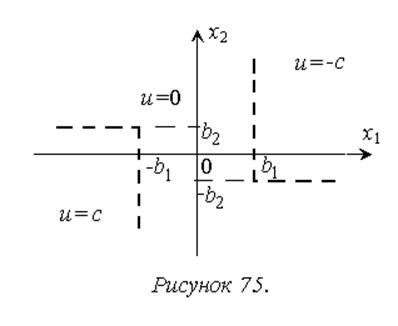
Теперь учтем запаздывание при включении и выключении двигателей. Вертикальные линии переключения, как и ранее, повернутся по часовой стрелке на угол , где t - время запаздывания. Горизонтальные линии также изменят свое положение. При достижении фазовыми траекториями горизонтальных линий переключения двигательные установки включены и объект управления движется с постоянным угловым ускорением  в левой полуплоскости и  в правой. Следовательно, после достижения линии переключения x₂=b₂ в левой полуплоскости до момента выключения двигателей изображающая точка сместится вверх на расстояние Dx₂=ct, причем независимо от величины своей горизонтальной координаты. Таким образом, вся горизонтальная линия переключения в левой полуплоскости займет положение b₂+ct. Аналогично можно показать, что в правой полуплоскости уравнение горизонтальной линии переключения примет вид: x₂=-b₂-ct, что эквивалентно смещению вверх на то же расстояние (рисунок 77).

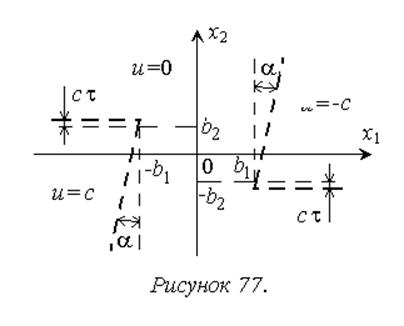
Фазовый портрет процессов в системе при логическом законе управления с учетом запаздывания, показанный на рисунке 78, демонстрирует наличие устойчивого предельного цикла.

В качестве особенности и достоинства логического закона отметим, что предельный цикл достигается не асимптотически, а в течение не более одного колебания. Логический закон управления превосходит обычные линейные законы с точки зрения быстродействия. Если при этом амплитуда достигаемого автоколебательного процесса не превышает допустимых значений, его следует признать предпочтительным.