Лекция 18. Основные сведения о математическом аппарате, применяемом для импульсных и дискретных систем
 Математическая модель
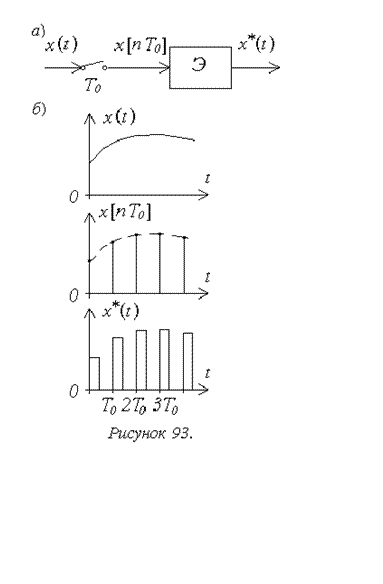
импульсного элемента обычно рассматривается в форме последовательного
соединения ключа, замыкающегося и размыкающегося с периодом T0,
и непрерывной части (рисунок 93а). Принимается, что ключ замыкается на
время, значительно меньшее по сравнению с T0. Поэтому
сигнал на выходе ключа может рассматриваться как решетчатая функция (рисунок 93б),
значения которой совпадают со значениями входного сигнала x(t) в
моменты времени t=nT0, где n=0,1,2,...
Непрерывная часть импульсного элемента (экстраполятор) обеспечивает
формирование импульсов определенной формы и длительности.
Математическая модель
импульсного элемента обычно рассматривается в форме последовательного
соединения ключа, замыкающегося и размыкающегося с периодом T0,
и непрерывной части (рисунок 93а). Принимается, что ключ замыкается на
время, значительно меньшее по сравнению с T0. Поэтому
сигнал на выходе ключа может рассматриваться как решетчатая функция (рисунок 93б),
значения которой совпадают со значениями входного сигнала x(t) в
моменты времени t=nT0, где n=0,1,2,...
Непрерывная часть импульсного элемента (экстраполятор) обеспечивает
формирование импульсов определенной формы и длительности.
 Несмещенная решетчатая функция f[nT0],
в сокращенной записи f[n], - это функция, значения которой
определены в дискретные моменты времени t=nT0, где n -
номер такта, T0=const - период дискретности.
Несмещенная решетчатая функция может быть получена из непрерывной функции, как
видно из рисунка 93б, на основе соотношения:
Несмещенная решетчатая функция f[nT0],
в сокращенной записи f[n], - это функция, значения которой
определены в дискретные моменты времени t=nT0, где n -
номер такта, T0=const - период дискретности.
Несмещенная решетчатая функция может быть получена из непрерывной функции, как
видно из рисунка 93б, на основе соотношения: 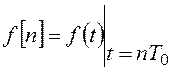 .
Смещенная решетчатая функция определяется в смещенные относительно начала такта
моменты времени:
.
Смещенная решетчатая функция определяется в смещенные относительно начала такта
моменты времени: 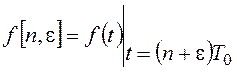 , где e - смещение, 0<e<1. Для решетчатых
функций могут выполняться все операции, аналогичные операциям с непрерывными
функциями: дифференцирование, интегрирование и др.
, где e - смещение, 0<e<1. Для решетчатых
функций могут выполняться все операции, аналогичные операциям с непрерывными
функциями: дифференцирование, интегрирование и др.
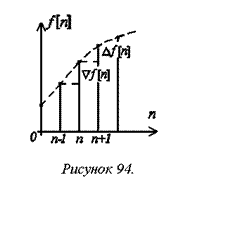
Роль первой производной непрерывной функции для решетчатой функции может выполнять первая прямая разность (рисунок 94)
![]()
или первая обратная разность
![]() .
.
Прямая разность определяется для момента времени t=nT0 с учетом будущего значения решетчатой функции при t=(n+1)T0. Это можно сделать, когда будущее значение известно. Обратную разность можно определить всегда, так как она определяется с учетом прошлого значения решетчатой функции при t=(n-1)T0 .
Роль второй производной для решетчатой функции выполняют вторая прямая разность
![]()
или вторая обратная разность
![]() .
.
Высшие прямая и обратная разности определяются с помощью рекуррентных соотношений:
![]() , (18.1)
, (18.1)
![]() .
.
При вычислении обратных разностей значения f[m] для m<0 следует брать равными нулю.
Роль определенного интеграла для решетчатой функции могут выполнять неполная сумма
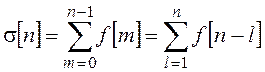
или полная сумма
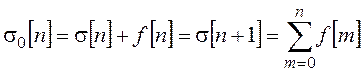 .
.
Для смещенных решетчатых функций все перечисленные соотношения аналогичны.
В качестве аналогов дифференциальных уравнений для решетчатых функций используются разностные уравнения (уравнения в конечных разностях). Для прямых разностей может быть составлено неоднородное линейное разностное уравнение
![]() , (18.2)
, (18.2)
где y[n] - искомая, f[n] - заданная решетчатые функции. На основе (18.1) уравнение (18.2) может быть преобразовано к виду:
![]() . (18.3)
. (18.3)
Для обратных разностей уравнения будут иметь вид:
![]() ,
,
![]() . (18.4)
. (18.4)
Наиболее удобны уравнения вида (18.3) и (18.4), так как они легко преобразуются в рекуррентные формулы для пошагового вычисления решетчатой функции y[n], удобные для реализации на компьютере:
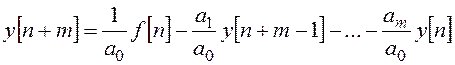 ,
,
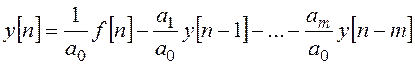 .
.
При f[n]=0 получим однородные разностные уравнения. Их решение может быть получено аналогично решению однородных дифференциальных уравнений. Составляется характеристическое уравнение:
![]() (18.5)
(18.5)
и определяются его корни zi , i=1,2,...,m.
Общее решение однородного разностного уравнения при вещественных некратных корнях характеристического уравнения имеет вид:
![]() , (18.6)
, (18.6)
где Ci – произвольные постоянные, определяемые через начальные условия.
Вещественному корню zj кратности k будет соответствовать составляющая общего решения:
![]() , (18.7)
, (18.7)
Паре комплексно сопряженных корней - следующая составляющая:
![]() , (18.8)
, (18.8)
где r – модуль, j – аргумент комплексного корня z=a+ b; C, y – произвольные постоянные, определяемые через начальные условия.
Поскольку общее решение уравнения системы описывает ее свободное движение, или переходную составляющую процесса в системе, то из (18.6)-(18.8) следует, что для асимптотической устойчивости системы, описываемой разностным уравнением, необходимо и достаточно, чтобы корни характеристического уравнения (18.5) удовлетворяли условию:
![]() , i=1,2,...,m.
(18.9)
, i=1,2,...,m.
(18.9)
Так же, как и для линейных непрерывных систем, при исследовании устойчивости импульсных систем желательно избежать трудоемкой процедуры вычисления корней характеристического уравнения. Это обеспечивается на основе специальных преобразований решетчатых функций, позволяющих и для импульсных систем применить аппарат передаточных функций, частотных характеристик и так далее.
Второй вариант математического описания импульсного звена (рисунок 93) предполагает, что на выходе ключа формируется последовательность d-функций, площадь каждой из которых совпадает со значением входного сигнала звена x(t) в моменты времени t=nT0:
x*[n] =x(t)d(t-nT0), n=0,1,2,...
Здесь и ниже ограничимся рассмотрением несмещенных решетчатых функций.
Дискретное преобразование Лапласа решетчатой функции f[n] определяется формулой:
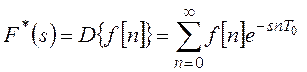 . (18.10)
. (18.10)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.