Основные сведения о математическом аппарате, применяемом для импульсных и дискретных систем, страница 2

Как видно из (18.10), изображение F^*(s) является функцией величины .

На основе подстановки  может быть получено более удобное для решения практических задач z-преобразование:

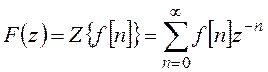.                           (18.11)

Таким образом, изображения F ^*(s) и F(z) взаимно однозначно связаны. Переход от одного из них к другому или обратно осуществляется путем указанной подстановки.

Z-преобразование может быть выполнено и для непрерывной функции времени:

.

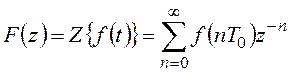В таблице 1 приведены некоторые часто встречающиеся при математическом описании процессов управления функции времени, а также соответствующие им решетчатые функции и изображения.

Отметим, что при исследовании импульсных систем роль d-функции выполняет единичная импульсная функция:

.

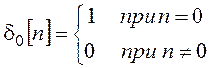Свойства дискретного преобразования Лапласа и z-преобразования одинаковы. Рассмотрим их на основе z-преобразования.

Свойство линейности:

.

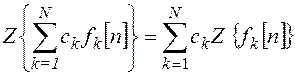Теорема смещения:

,  .

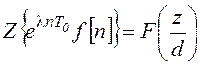Изображение первой прямой разности:

.

Изображения прямых разностей второго и более высоких порядков имеют сложный вид и неудобны для практического использования.

Для обратных разностей, благодаря f[m]=0 для m<0, изображения имеют простой вид:

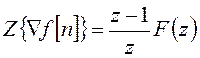,                                     (18.12)

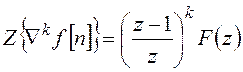.                                 (18.13)

Отметим, что соотношения (18.12), (18.13) аналогичны теоремам дифференцирования для непрерывного преобразования Лапласа в случае нулевых начальных условий.

Изображение неполной суммы:

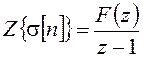,                                      (18.14)

а для k-кратной суммы

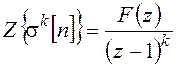.                                  (18.15)

Для полной суммы соответственно:

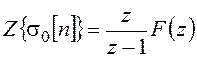,                                  (18.16)

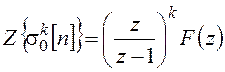.                                (18.17)

Соотношения (18.14) - (18.17) аналогичны теоремам интегрирования для непрерывного преобразования Лапласа в случае нулевых начальных условий.

Таблица 1.

Непрерывная функция f(t)	Непрерывное изображение по Лапласу F(s)	Решетчатая функция f[n]	Z-изображение F(z)
	-		1
1(t)		1[n]
1(t) - 1(t-T0)			1
t		nT0
			,

На основе соотношений (18.12) - (18.17) можно увидеть, что величина 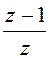 для дискретного преобразования Лапласа является аналогом оператора  s  для непрерывного преобразования Лапласа.

Теорема о конечном значении решетчатой функции:

.

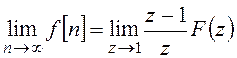Теорема о начальном значении решетчатой функции:

.

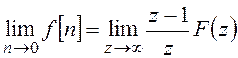Свертка решетчатых функций:

.

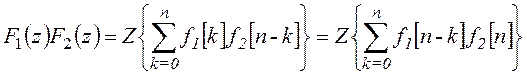Для решетчатой функции, сдвинутой вправо на целое число тактов m, изображение может быть найдено на основе теоремы запаздывания:

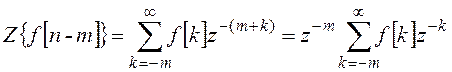
и далее с учетом  f[k]=0 для k<0:

.                      (18.17)

На основе теоремы запаздывания можно построить процедуру перехода от разностных уравнений к алгебраическим уравнениям для z-изображений решетчатых функций и далее к передаточным функциям, аналогичную известной для дифференциальных уравнений.

Рассмотрим линейное разностное уравнение, полученное на основе обратных разностей, в наиболее общем виде:

.

Принимая f[k]=0 и y[k]=0 для k<0 и используя (18.16), получим:

.

Теперь изображение искомой решетчатой функции Y(z) можно выразить через изображение заданной для правой части уравнения решетчатой функции F(z):

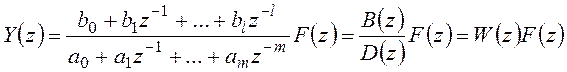.        (18.18)

Таким образом введена дискретная передаточная функция W(z) как отношение изображений выходной и входной переменных

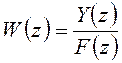
при нулевых начальных условиях. Для дискретных систем она играет такую же роль, как и обычная передаточная функция для непрерывных систем. Как и для обычной передаточной функции, знаменатель  взаимно однозначно соответствует левой части разностного уравнения, а числитель  - правой части.

В заключение перечислим способы решения разностных уравнений, вытекающие из изученного материала.

1. Классический метод решения разностного уравнения

дает решение в форме:

y[n]=y_п[n]+y_в[n], где y_п[n] – переходная составляющая (свободное движение) находится как общее решение уравнения в соответствии с (18.5)-(18.8), y_в[n] – вынужденная составляющая – находится как частное решение уравнения.

2. Использование рекуррентных формул:

.

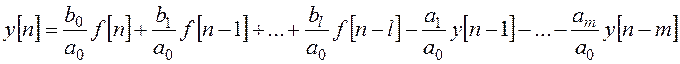3. Переход от изображения известной (заданной) функции F(z) к изображению искомой функции Y(z) на основе (18.18) и использование таблиц z-изображений для получения оригинала y[n]. Если изображение Y(z) получается сложным и не содержится в таблицах, его раскладывают в сумму табличных изображений и получают результат в виде суммы оригиналов в соответствии со свойством линейности z-преобразования.