Статистической линеаризацией называется построение линейной модели нелинейного звена системы управления с учетом характеристик преобразования случайного сигнала линейной частью системы.
Методы статистической линеаризации основаны на
допущении о наличии у линейной части системы свойства фильтра. Благодаря этому,
сигнал на входе нелинейного звена, то есть на выходе линейной части,
рассматривается в форме ![]() ,
причем для описания центрированной составляющей ограничиваются дисперсией Dx или среднеквадратическим отклонением
,
причем для описания центрированной составляющей ограничиваются дисперсией Dx или среднеквадратическим отклонением ![]() .
.
Замена нелинейного звена линеаризованной моделью позволяет использовать принцип суперпозиции - провести раздельный анализ преобразования системой детерминированных и случайных составляющих входных сигналов. Особенность применения принципа суперпозиции на основе статистической линеаризации состоит в том, что для случайных составляющих нелинейное звено заменяется безынерционным звеном с коэффициентомk1, а для детерминированных - безынерционным звеном с коэффициентом k0 (при нечетной нелинейности) или постоянным сигналом j0.
Коэффициенты статистической линеаризации оказываются функциями моментов распределения сигналов на входе нелинейности, которые, в свою очередь, вычисляются через передаточные функции системы, включающей в себя линеаризованное звено, то есть зависят от коэффициентов статистической линеаризации. Вследствие этого расчет стационарного процесса в статистически линеаризованной системе сводится к решению системы нелинейных алгебраических уравнений, требующему применения численных методов.
Таким образом, если на вход нелинейного звена со статической характеристикой y = F(x), действует сигнал, представляющий собой случайный процесс в виде:
![]() , (1)
, (1)
где
![]() – математическое ожидание, которое
является обычной (регулярной) функцией времени,
– математическое ожидание, которое
является обычной (регулярной) функцией времени,
![]() – случайная центрированная составляющая.
– случайная центрированная составляющая.
Процесс на выходе нелинейного звена приближенно может быть представлен в виде:
![]() , (2)
, (2)
где
![]() ,
, ![]() – коэффициенты
статистической линеаризации.
– коэффициенты
статистической линеаризации.
В нашем случае (для идеальной релейной характеристики) значения этих коэффициентов следующие:
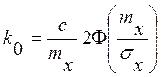 , (3)
, (3)
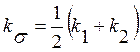 , (4)
, (4)
где 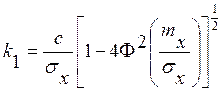 ,
(5)
,
(5)
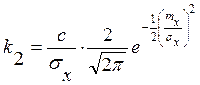 .
(6)
.
(6)
В соответствии с формулой (4) получим:
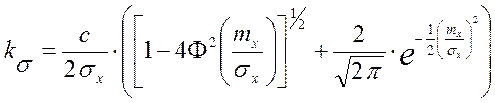 . (7)
. (7)
Далее будем обозначать ![]() .
.
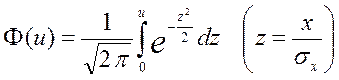 , (8)
, (8)
где
![]() –
интеграл вероятности для нормально распределенного входного сигнала.
–
интеграл вероятности для нормально распределенного входного сигнала.
Для расчёта детерминированной составляющей сигнала ошибки после линеаризации используется следующая структурная схема (рисунок 2).
|
|
|
|
|
|
|
|
|
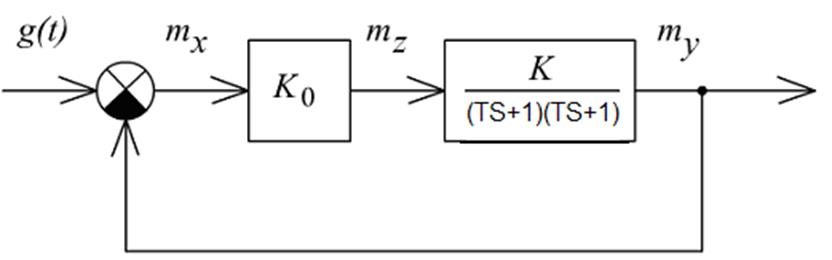
Рисунок 2
Найдём значение математического ожидания по формуле (9):
![]() , (9)
, (9)
где
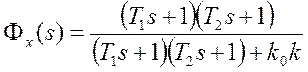 – передаточная функция замкнутой
системы по ошибке,
– передаточная функция замкнутой
системы по ошибке,
Задающее воздействие:
![]() . (10)
. (10)
Изображение по Лапласу задающего воздействия (10) имеет вид:
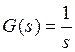 , (11)
, (11)
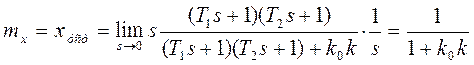 . (12)
. (12)
Для расчета центрированной случайной составляющей используется структурная схема (рисунок 3)
|

Рисунок 3
Дисперсия принимает значение в соответствии с формулой (13).
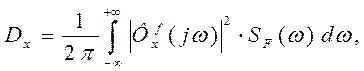
(13)
где
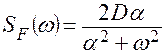 – спектральная плотность помехи
– спектральная плотность помехи ![]() .
.
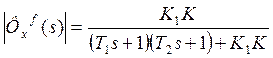 . (14)
. (14)
При замене в (14) s = jω, получим:
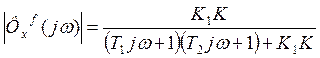 , (15)
, (15)
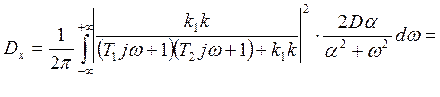
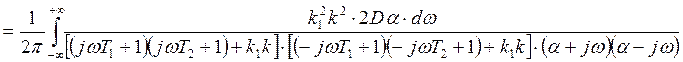 . (16)
. (16)
Для нахождения данного интеграла в формуле (16) воспользуемся следующей формулой:
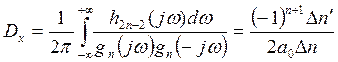 . (17)
. (17)
В нашем случае:
![]() , (18)
, (18)
![]() . (19)
. (19)
Коэффициенты полинома (18):
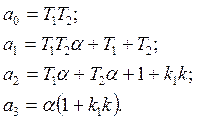
Коэффициенты полинома (19):
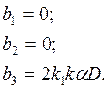
Вычислим определители:
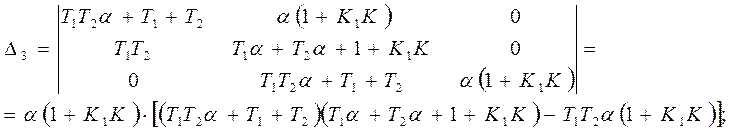 (20)
(20)
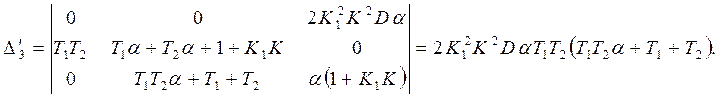 (21)
(21)
Найдем дисперсию, подставив результаты (20) и (21) в формулу
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.