Практическое занятие 3.Расчет параметров автоколебаний и анализ их устойчивости частотным способом
Пример 1.
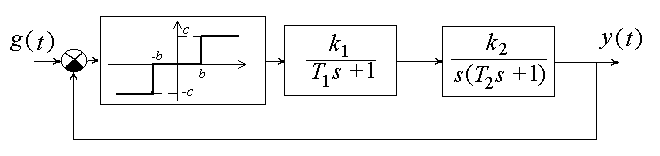
Исходные данные: g(t)=0; b=10; c=10; k=k1k2=20 c-1; T1=1 c; T2=0,1.
Проанализировать возможность автоколебаний в системе.
Частотная передаточная функция линейной части системы имеет вид:
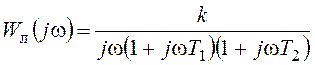 .
.
Выражения для АЧХ и ФЧХ:
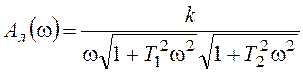 ,
,
![]() .
.
Для решения задачи потребуется представление ЧПФ в алгебраической форме:
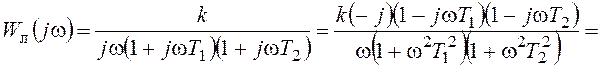
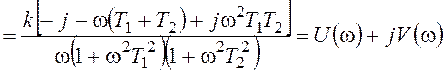 ,
,
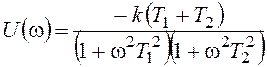 ,
, 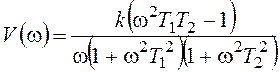 .
.
Коэффициенты
гармонической линеаризации нелинейности: 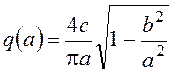 , существует при a≥b, q’(a)=0.
Передаточная функция линеаризованной нелинейной части:
, существует при a≥b, q’(a)=0.
Передаточная функция линеаризованной нелинейной части: 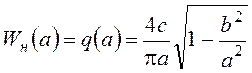 - вещественная
функция. График ее зависимости от амплитуды колебаний показан на рисунке.
- вещественная
функция. График ее зависимости от амплитуды колебаний показан на рисунке.
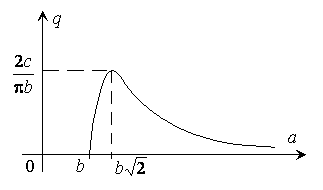
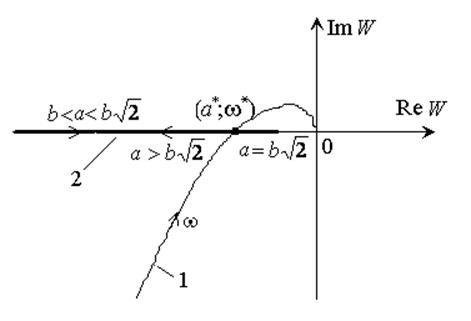
Годографы, соответствующие левой и правой частям уравнения
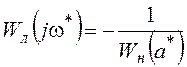 , показаны
на рисунке: 1 – АФХ линейной части; 2 – годограф функции
, показаны
на рисунке: 1 – АФХ линейной части; 2 – годограф функции 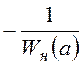 .
.
Составим уравнения для определения параметров
предельного цикла 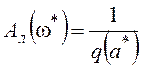 и
и
![]() :
:
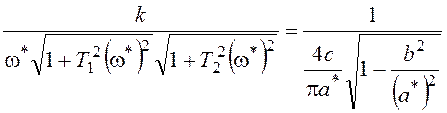 ;
;
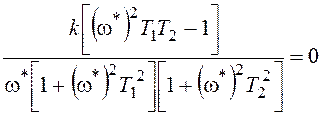 ,
, ![]() .
.
Последнее уравнение позволяет найти частоту
предельного цикла: 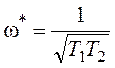 . После подстановки ее в первое
уравнение получим:
. После подстановки ее в первое
уравнение получим:
 .
.
Данное уравнение приводится к виду, рассмотренному в аналогичном примере на предыдущем занятии:
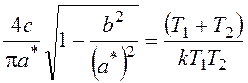 .
.
Его решение и анализ поведения системы при различных условиях, очевидно, также аналогичны, за исключением анализа устойчивости предельных циклов.
Из рисунка видно, что имеют место два решения – с одинаковой частотой и разными амплитудами. Расчеты показывают: w*=3,16, a1*=11,6; a2*=20.
Амплитуда a1 относится к
диапазону ![]() . В этом диапазоне увеличению параметра a соответствует
движение по годографу 2 к началу координат. Следовательно, предельный цикл с
амплитудой a1 неустойчив.
. В этом диапазоне увеличению параметра a соответствует
движение по годографу 2 к началу координат. Следовательно, предельный цикл с
амплитудой a1 неустойчив.
Амплитуда a2 относится к
диапазону ![]() . В этом диапазоне увеличению параметра a соответствует
движение по годографу 2 от начала координат. Следовательно, предельный цикл с
амплитудой a2 устойчив.
. В этом диапазоне увеличению параметра a соответствует
движение по годографу 2 от начала координат. Следовательно, предельный цикл с
амплитудой a2 устойчив.
Пример 2.
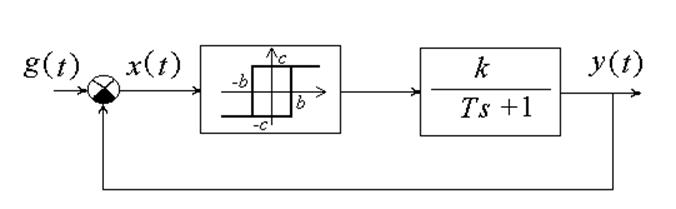
Исходные данные: g(t)=0.
Проанализировать возможность автоколебаний в системе.
Частотная передаточная функция линейной части системы имеет вид:
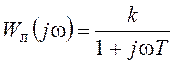 .
.
АФХ линейной части показана на рисунке.
ЧПФ линеаризованного нелинейного звена:
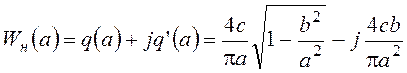 .
.
Обратная ЧПФ линеаризованного нелинейного звена со знаком «-»:
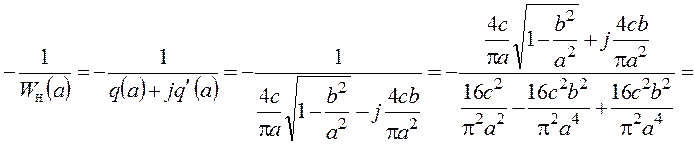
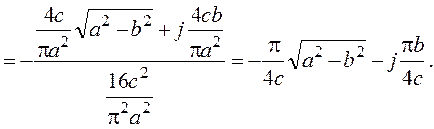
Годограф данного выражения показан на рисунке.
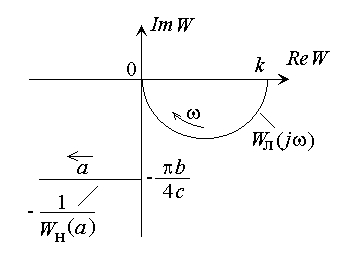
Поскольку кривые на рисунке не пересекаются, метод гармонической линеаризации не позволяет обнаружить для данной системы какой-либо предельный цикл.
Имитационное моделирование процессов в рассматриваемой системе, тем не менее, позволяет в ряде случаев в зависимости от начальных условий и значений параметров звеньев системы обнаружить наличие автоколебаний.
При этом проверка наличия свойства фильтра для тех же параметров дает отрицательный результат.
Этот пример демонстрирует границы применимости рассматриваемого приближенного метода.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.