ДОМАШНЕЕ ЗАДАНИЕ № 3
Определение автоколебаний нелинейной САУ
Исследовать устойчивость состояния равновесия нелинейных систем, структурные схемы которых приведены ниже.
Еслив системе устанавливаются автоколебания, то определить их амплитуду и частоту на выходе системы.
Параметры линейной части СУ и статической характеристики нелинейного звена (НЭ) указаны в таблицах после соответствующих схем.
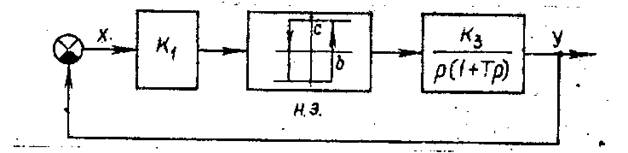
Схема 1
|
Параметры |
Варианты |
||||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
|
|
1,0 |
2,0 |
3,0 |
4,0 |
5,0 |
6,0 |
7,0 |
8,0 |
9,0 |
10 |
5,0 |
6,0 |
5,0 |
4,0 |
5,0 |
|
|
20 |
18 |
16 |
14 |
12 |
10 |
8,0 |
6,0 |
4,0 |
2,0 |
2,0 |
4,0 |
4,0 |
2,0 |
5,0 |
|
|
3,0 |
2,5 |
2,0 |
1,5 |
1,6 |
1,0 |
2,0 |
2,5 |
3,0 |
3,5 |
2,0 |
1,0 |
2,0 |
5,0 |
2,0 |
|
Т, с |
0,3 |
0,25 |
0,2 |
0,15 |
0,1 |
0,1 |
0,15 |
0,2 |
0,25 |
0,3 |
0,145 |
0,33 |
0,25 |
0,5 |
0,125 |
где b = 0,1В - ширина гистерезисной петли, В; С - уровень сигнала на выходе нелинейного элемента, В; K1, K2, K3 коэффициенты передачи звеньев; Т - постоянная времени.
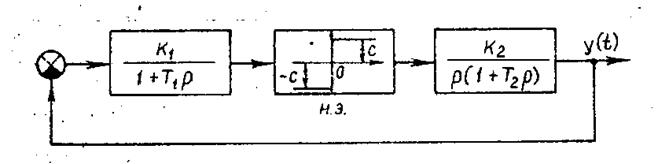
Схема 2.
|
Параметры |
Варианты |
||||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
|
|
5,0 |
4,0 |
3,0 |
4,0 |
10 |
2,0 |
5,0 |
5,0 |
6,0 |
6,5 |
8,0 |
10 |
5,0 |
4,5 |
5,0 |
|
Кн |
1,0 |
1,0 |
2,5 |
2,0 |
1,0 |
1,2 |
2,0 |
3,0 |
2,2 |
1,5 |
3,0 |
2,0 |
3,0 |
1,8 |
2.0 |
|
|
2,0 |
2,0 |
2,0 |
1,5 |
2,0 |
11 |
2,5 |
2,0 |
3,0 |
2,8 |
1,5 |
2,0 |
3,0 |
6,0 |
5,0 |
|
Т1, с |
3,0 |
2,6 |
2,4 |
2,0 |
1,8 |
1,6 |
1,4 |
1,2 |
0,8 |
0,6 |
0,5 |
0,4 |
0,3 |
0,2 |
0,3 |
|
Т2, с |
1,2 |
1,0 |
0,8 |
0,6 |
0,5 |
0,4 |
0,45 |
0,3 |
0,2 |
0,25 |
0,15 |
0,1 |
0,15 |
0,05 |
0,01 |
где K1, K2 - коэффициенты передачи звеньев; Т1, Т2- постоянные времени; С - уровень сигнала на выходе нелинейного элемента, В; Кн - коэффициент передачи (Кн=С). Если в системе устанавливаются автоколебания, то определись их амплитуду и частоту на выходе системы.
Методические указания
1. Определение параметров автоколебаний в нелинейной системе и исследование устойчивости периодического решения провести двумя способами: используя критерий Михайлова и критерий Найквиста.
2. К домашнему заданию должны быть приложены два графика: 1) поясняющий применение критерия Михайлова для исследования устойчивости периодического решения; 2) поясняющий применение критерия Найквиста для определения параметров автоколебаний в исследуемой системе.
3. Устойчивость периодического решения должна быть проверена также применением аналитического критерия устойчивости.
Литература
1. АндриевскийА.Б., АндриевскийБ.Р., ЕмельяновВ.Ю., КоротковБ.Ф. Теория управления: лабораторный практикум в среде Scilab. – СПб: БГТУ, 2008 (электронная версия).
2. БесекерскийВ.А., ПоповЕ.П. Теория систем автоматического управления. - СПб: Профессия, изд. 4, 2003.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.