Понятие абсолютной устойчивости нелинейных систем, Частотный критерий абсолютной устойчивости

Лекция 7. Понятие абсолютной  устойчивости нелинейных систем. Частотный критерий абсолютной устойчивости

Основные понятия устойчивости, введенные для линейных систем, применимы и к нелинейным системам. Прежде всего, понятие устойчивости по Ляпунову.

Формулировка понятия устойчивости по Ляпунову основана на понятиях возмущенного и невозмущенного движения системы, которые рассматриваются в двух вариантах: для переменных состояния системы и в отклонениях.

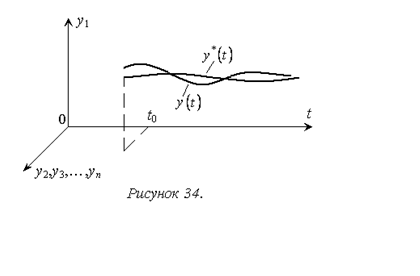В первом случае (рисунок 34) рассматриваются законы изменения переменных состояния системы в установившемся процессе, в частном случае их значения в состоянии равновесия, , i=1,2,…,n, - по Ляпунову это невозмущенное движение. Возмущенное движение y_i(t), i=1,2,…,n,  – это законы изменения переменных состояния системы в переходном процессе, то есть свободное движение системы после начального отклонения, вызванного любыми причинами. Такая трактовка движения системы является наиболее общей и позволяет различать варианты невозмущенного движения в случае, если для рассматриваемой нелинейной системы их два и более.

Во втором случае возмущенное движение вводится как отклонение . При такой трактовке невозмущенное движение имеет вид . Такая трактовка более удобна для анализа процессов в системе.

Невозмущенное движение системы (установившийся процесс)  называется устойчивым, если при заданном сколь угодно малом e>0 существует такое d=d(e)>0, что при начальных условиях , i=1,2,…,n существует такое t₁>t₀, что при t₁<t<∞ выполняется условие , i=1,2,…,n, то есть возмущенное движение ограничено.

Если условия определения устойчивости по Ляпунову выполняются, и , то соответствующее невозмущенное движение  называется асимптотически устойчивым.

Если  после любых начальных отклонений, то есть независимо от выполнения условий устойчивости по Ляпунову, то система, или процесс в системе, называются асимптотически устойчивыми в целом.

Пример 2, рассмотренный на практических занятиях по методу гармонической линеаризации, пример системы, для которой при k>k_гр невозмущенное движение асимптотически устойчиво при начальных условиях в малом диапазоне относительно . В таких случаях говорят, что состояние равновесия устойчиво «в малом» и неустойчиво «в большом». Если для системы имеется только одно возможное состояние равновесия, говорят об устойчивости системы «в малом».

Для нелинейных систем существует также  понятие абсолютной устойчивости, отличающееся от одноименного понятия для линейных систем.

Абсолютная устойчивость означает асимптотическую устойчивость системы в целом при любом характере нелинейности внутри определенного класса нелинейностей. Например, может рассматриваться вопрос об абсолютной устойчивости при наличии в системе любой нечетной нелинейности, любой однозначной нелинейности и пр.

Частотный критерий абсолютной устойчивости В.М. Попова дает достаточные условия абсолютной устойчивости нелинейной системы по виду АФХ ее линейной части.

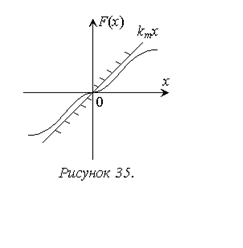
Рассмотрим сначала случай, когда в системе присутствует однозначная нелинейность со статической характеристикой, удовлетворяющей условию: