Частотный (графический) способ расчета параметров автоколебаний и анализа их устойчивости

Лекция 6. Частотный (графический) способ расчета параметров автоколебаний и анализа их устойчивости

Основой данного способа, как и алгебраического, является линеаризованная модель системы (рис. 28), где

,

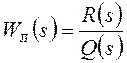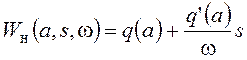
для случая симметричных колебаний. Получим частотную передаточную функцию разомкнутой системы для предусматриваемого критерием устойчивости Найквиста случая единичной отрицательной обратной связи:

,

.

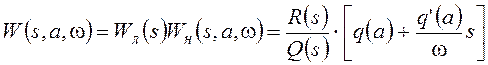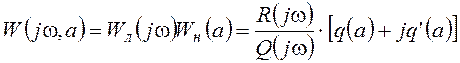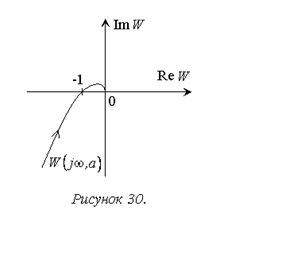Условие нахождения системы на колебательной границе устойчивости, получаемое по критерию Найквиста (рис. 30):

или (рис. 31)

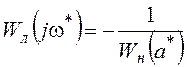,                 (6.1)

гдеa^* и w^* являются параметрами предельного цикла для данной нелинейной системы.

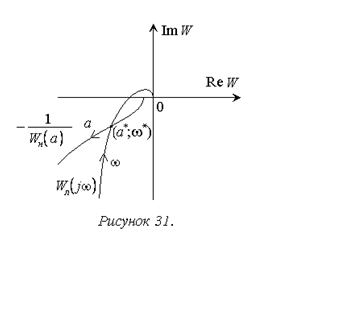В соответствии с (6.1) периодические решения (предельные циклы) соответствуют точкам пересечения АФХ линейной части системы и обратной АФХ линеаризованной нелинейной части со знаком «-». Удобство здесь состоит в том, что для построения первой из них параметром является частота, второй – амплитуда. То есть кривые строятся независимо друг от друга и точкам их пересечения однозначно соответствуют пары (a^*;w^*).

Рассматривая по отдельности модули и аргументы выражений в уравнении (6.1), получим следующие расчетные уравнения:

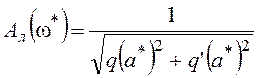,                                       (6.2)

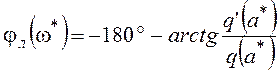.                                       (6.3)

Вместо (6.2) может использоваться уравнение для ЛАХ:

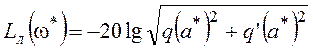.                                     (6.4)

Для однозначной нечетной нелинейности q'(a)=0 и 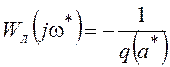. Поэтому уравнения упрощаются:

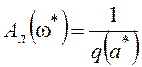 или ;                              (6.5)

 или .                                      (6.6)

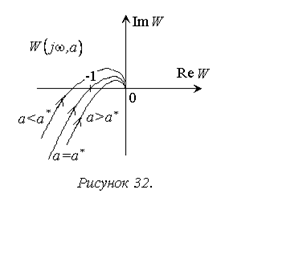
Для получения условий устойчивости предельного цикла с параметрами a=a^* и w=w^* учтем, что в переходном процессе, по крайней мере, в малой окрестности устойчивого предельного цикла, колебания с амплитудой a>a^* должны затухать, а с амплитудой a<a^* - расходиться. Следовательно, при a>a^* АФХ разомкнутой системы, показанная на рисунке 30, должна деформироваться так, чтобы критерий устойчивости Найквиста выполнялся, при a<a^* - нарушался (рис. 32).

Для практического применения более удобен анализ взаимного расположения АФХ линейной части системы и обратной АФХ линеаризованной нелинейной части, не требующий дополнительных построений. Из рис. 32 следует, что для устойчивости предельного цикла требуется, чтобы при a>a^* выполнялось неравенство:

 или 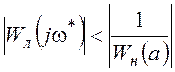, то есть годограф функции  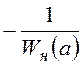в окрестности точки пересечения с АФХ линейной части должен удаляться от начала координат при увеличении своего аргумента a. В соответствии с этим условием отметим, что годографы на рис. 31 соответствуют устойчивому предельному циклу.

Исследование устойчивости предельного цикла графическим способом может быть выполнено и на основе кривой Михайлова с использованием аналогичных соображений.

В качестве примера применения графического способа рассмотрим САУ, ранее исследованную алгебраическим способом (рис. 29).

Частотная передаточная функция линейной части системы имеет вид:

.

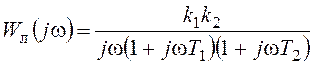Выражения для АЧХ и ФЧХ:

,

.

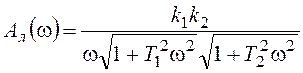Коэффициенты гармонической линеаризации нелинейности: 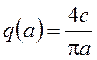, q’(a)=0. Соответственно 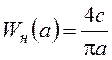,  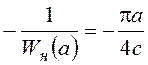- вещественные функции.

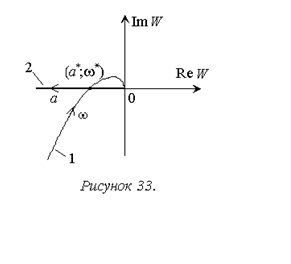
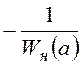Годографы  (кривая 1) и  (кривая 2) представлены на рис. 33.

Составим и решим уравнения (6.5)-(6.6), учитывая, уравнение для ФЧХ менее удобно для решения:

;

,

;

,  ;

, .

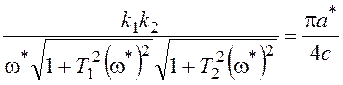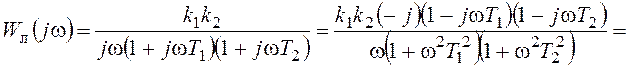
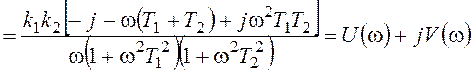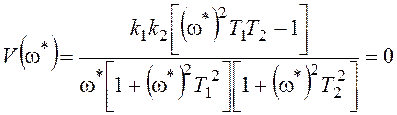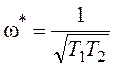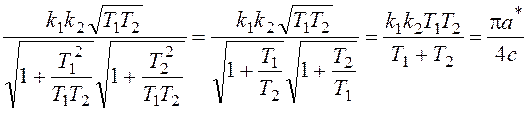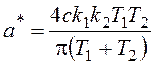Устойчивость найденного предельного цикла подтверждается направлением увеличения параметра a на годографе 2 (рис. 33).