Практическое занятие 5.Расчет характеристик стационарного случайного процесса в СУ
Пример 1. Задана корреляционная функция случайного процесса
Kx(t)=Dxe -a|t |.
Найти его спектральную плотность.
Воспользуемся преобразованием Фурье:
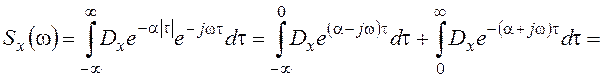
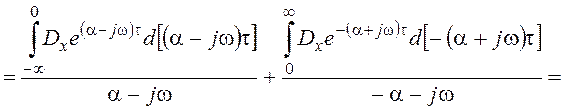
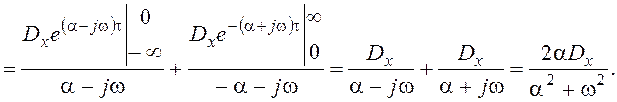
Для лучшего понимания смысла и взаимосвязи рассматриваемых характеристик обратимся к их графикам для рассмотренного примера.
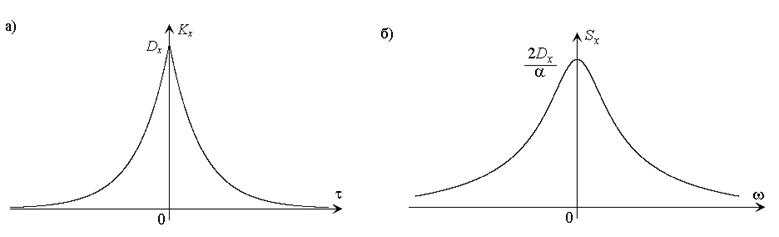
При увеличении степени взаимной зависимости (корреляции) значений процесса, разделенных интервалом времени t, значения Kx(t) возрастают, то есть при фиксированной Dx параметр a, определяющий скорость снижения Kx(t), убывает.
По полученному выше выражению можно убедиться в том, что график спектральной плотности претерпит изменения противоположного характера: значение Sx(0) увеличится, крутизна графика при увеличении частоты возрастет. Физический смысл такого эффекта состоит в том, что при увеличении степени корреляции значений процесса, разделенных некоторым интервалом времени, менее вероятным становится быстрое изменение значения процесса, то есть снижается доля колебаний высоких частот.
Дальнейшее увеличение степени корреляции значений процесса в пределе даст детерминированный процесс (Kx(t)=const, спектральная плотность примет вид d-функции или суммы d-функций, линейчатого спектра).
Противоположный предельный случай – некоррелированный случайный процесс, белый шум:
Kx(t)=Gδ(t),
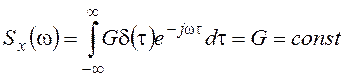 .
.
Пример 2. Построить формирующий фильтр для получения случайного процесса с корреляционной функцией Kx(t)=Dxe -a|t |.
Формирующим фильтром называется динамическое звено, обеспечивающее требуемые корреляционные свойства выходного сигнала.
Если на вход динамического звена поступает белый шум со спектральной плотностью Sx(w)=S0, спектральная плотность выходного сигнала X(t) будет определяться через частотную передаточную функцию звена W(jw) следующим образом:
Sx(w)=|W(jw)|2S0.
Необходимая передаточная функция формирующего фильтра определяется из соотношения:
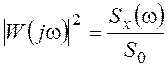 , где
, где
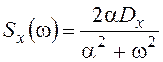
получена в примере 1.
Теперь найдем передаточную функцию формирующего фильтра:
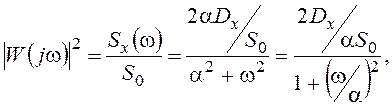
откуда
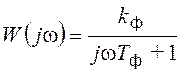 или
или 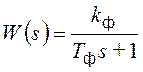 , где
, где 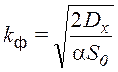 ,
, 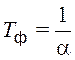 .
.
Такой формирующий фильтр может быть физически реализован, например, в виде четырехполюсника или на операционном усилителе. Для четырехполюсника kф=1, Tф=RC; для операционного усилителя kф=R2/R1, Tф=R2C.
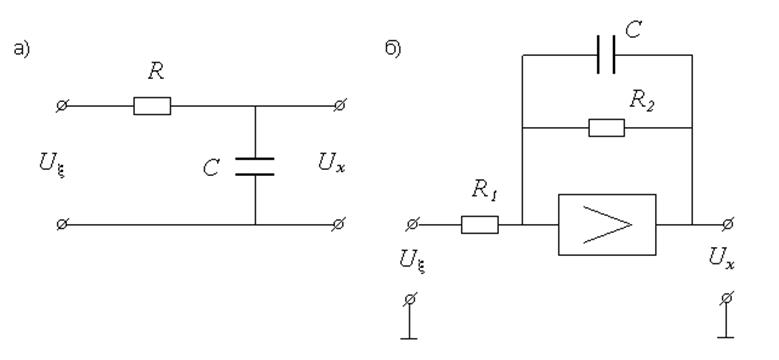
Пример 3.
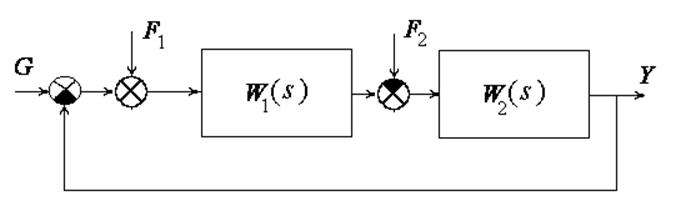
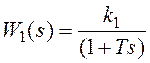 ,
, 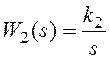 ,
k1=4, k2=5, T=0.2;
,
k1=4, k2=5, T=0.2;
mg(t)= t.1(t), Dg=0;
F1: mf(t)= 1(t), Df=0;
F2: mf(t)= 2.1(t), 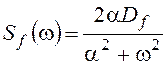 , Df =0.2, a=1.
, Df =0.2, a=1.
Найти математическое ожидание и дисперсию сигнала ошибки.
Получим необходимые передаточные функции:
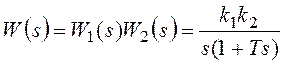 ,
,
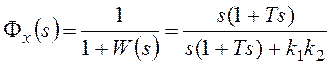 ;
;
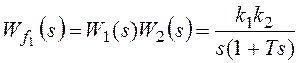 ,
,
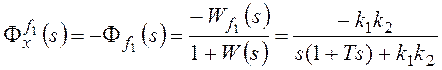 ;
;
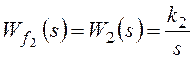 ,
,
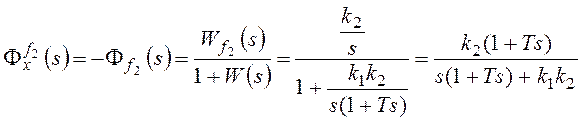 .
.
В соответствии с принципом суперпозиции математическое ожидание сигнала ошибки найдем как сумму
![]() ,
,
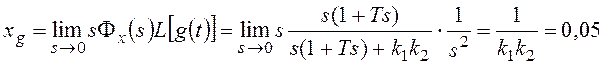 ,
,
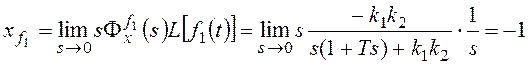 ,
,
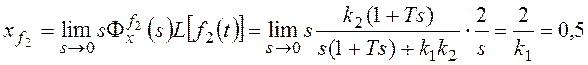 ,
,
mx=0,05–1+0,5=–0,45.
Случайная составляющая присутствует только у входного сигнала f2. Соответственно спектральная плотность сигнала ошибки:
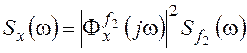
и дисперсия определяется следующим интегралом:
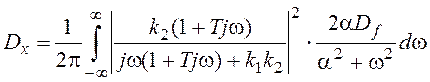 , который
необходимо привести к виду
, который
необходимо привести к виду
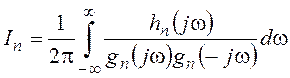 .
.
где hn(jω)=b1(jω)2n-2 +b2(jω)2n-4 +...+bn, gn(jω)=a0(jω)n +a1(jω)n-1 +...+an.
Выполним необходимые преобразования, учитывая, что:
![]() .
.
Тогда:
![]() ;
;
![]()
![]() .
.
Таким образом, n=3 и a0=T, a1=aT+1, a2=a+k1k2, a3=ak1k2, b1=0,
![]() ,
, ![]() .
.
Искомый интеграл вычисляется через определители третьего порядка:
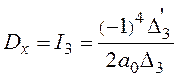 ,
,
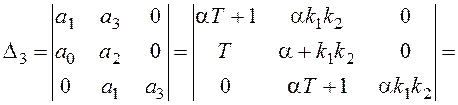
![]() ,
,
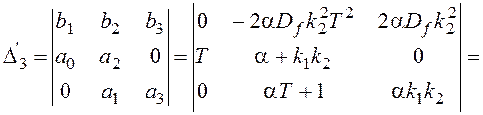
![]() ,
,
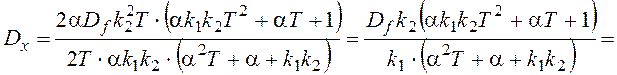
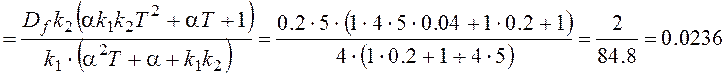 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.