Лекция 24. Синтез оптимального управления на основе вариационного исчисления
Среди вариационных задач, как и среди любого другого вида задач поиска экстремума выделяются задачи на безусловный и условный экстремумы. Рассмотрим сначала основные виды задач на безусловный экстремум.
Простейшая задача вариационного исчисления имеет
следующую постановку: требуется найти функцию x(t), определенную на интервале ![]() при
заданных значениях x(t0)=x0,
x(t1)=x1, доставляющую
экстремум функционалу вида:
при
заданных значениях x(t0)=x0,
x(t1)=x1, доставляющую
экстремум функционалу вида:
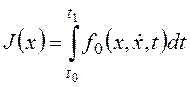 . (24.1)
. (24.1)
Иногда говорят, что требуется найти кривую x(t), концы которой закреплены в точках x(t0)=x0 и x(t1)=x1 (рисунок 112).
Первое необходимое условие достижения экстремума в простейшей задаче принимает вид уравнения Эйлера:
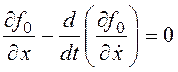 . (24.2)
. (24.2)
Уравнение Эйлера сводится к дифференциальному уравнению второго порядка относительно x(t). Его решение называют экстремалью. Далее с учетом граничных условий x(t0)=x0, x(t1)=x1 находят допустимую экстремаль (одну или несколько).
Второе необходимое условие достижения экстремума
принимает вид условия Лежандра: 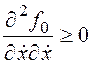 для
минимума или
для
минимума или 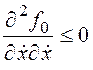 для максимума вдоль всей допустимой экстремали.
Условия Лежандра в форме строгих неравенств называются усиленными. Усиленное
условие Лежандра вместе с (24.2) образует достаточное условие минимума или
максимума функционала (24.1).
для максимума вдоль всей допустимой экстремали.
Условия Лежандра в форме строгих неравенств называются усиленными. Усиленное
условие Лежандра вместе с (24.2) образует достаточное условие минимума или
максимума функционала (24.1).
 Пример 1. Требуется обеспечить экстремум функционала
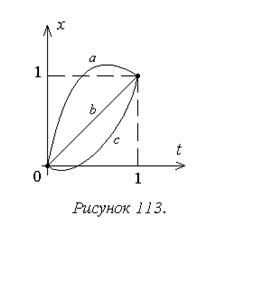
Пример 1. Требуется обеспечить экстремум функционала 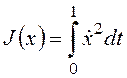 при граничных условиях x(0)=0, x(1)=1 (рисунок 113).
при граничных условиях x(0)=0, x(1)=1 (рисунок 113).
Найдем частные производные и составим уравнение Эйлера:
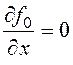 ,
, 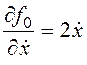 ;
;
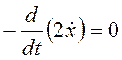 ,
, ![]() ,
, ![]() .
.
Уравнение экстремали получаем двойным интегрированием:
![]() , x=c1t+c2.
, x=c1t+c2.
С учетом граничных условий находим допустимую
экстремаль: x(0)=c2=0, x(1)=c1=1, ![]() .
.
Проверим выполнение условия Лежандра: 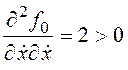 .
.
Таким образом, на кривой ![]() (кривая bна рисунке 113) обеспечивается минимум
величиной
(кривая bна рисунке 113) обеспечивается минимум
величиной 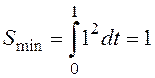 .
.
В векторном варианте простейшей задачи при X=(x1,x2,…,xn) и функционале вида
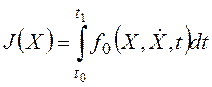 . (24.3)
. (24.3)
задаются граничные условия xi(t0)=xi0, xi(t1)=xi1, i=1,2,...,n.
Первое необходимое условие достижения экстремума здесь принимает вид системы уравнений Эйлера-Лагранжа:
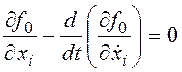 , i=1,2,....,n.
(24.4)
, i=1,2,....,n.
(24.4)
Второе условие (условие Лежандра) предусматривает анализ матрицы вторых частных производных
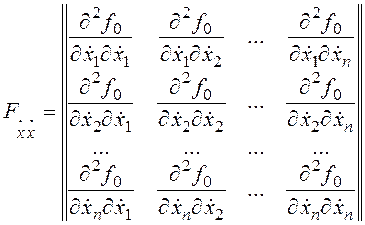 .
.
Условие Лежандра (необходимое условие): вдоль всей
допустимой экстремали матрица ![]() должна быть положительно полуопределенной
для минимума функционала и отрицательно полуопределенной для максимума.
должна быть положительно полуопределенной
для минимума функционала и отрицательно полуопределенной для максимума.
Усиленное условие Лежандра (достаточное условие): вдоль всей допустимой экстремали матрица ![]() должна быть
положительно определенной для минимума функционала и отрицательно определенной
для максимума.
должна быть
положительно определенной для минимума функционала и отрицательно определенной
для максимума.
В общем случае граничные условия могут быть заданы не полностью. В этом случае первое необходимое условие достижения экстремума (24.2) или (24.4) дополняется условиями трансверсальности. Рассмотрим возможные варианты.
 1. Задача с подвижными концами:
значения всех или некоторых составляющих векторной функции X при t=t0 или t=t1 не заданы
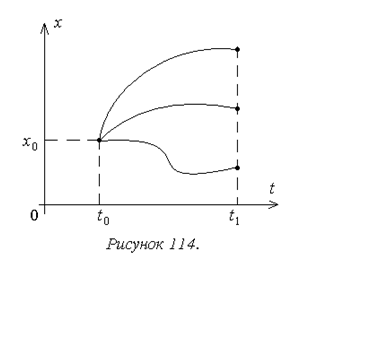
(концы частично не закреплены). Пример для одномерного случая, когда левый
конец закреплен, правый подвижен, представлен на рисунке 114. В таких задачах
первое необходимое условие достижения экстремума вместо каждого недостающего
граничного условия дополняется условием трансверсальности вида:
1. Задача с подвижными концами:
значения всех или некоторых составляющих векторной функции X при t=t0 или t=t1 не заданы
(концы частично не закреплены). Пример для одномерного случая, когда левый
конец закреплен, правый подвижен, представлен на рисунке 114. В таких задачах
первое необходимое условие достижения экстремума вместо каждого недостающего
граничного условия дополняется условием трансверсальности вида:
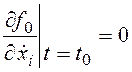 или
или
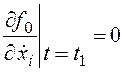 . (24.5)
. (24.5)
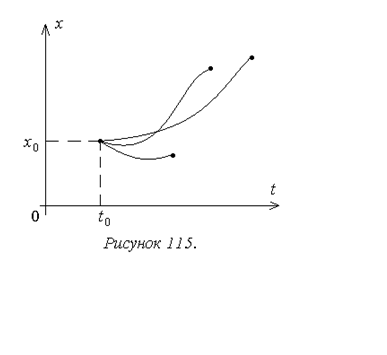 2. Задача со свободными
концами: не задана также граница временного интервала t0 или t1 (рисунок 115 – для одномерного случая правый конец
свободен). Вместо неопределенной границы первое необходимое условие достижения
экстремума дополняется условием трансверсальности соответственно:
2. Задача со свободными
концами: не задана также граница временного интервала t0 или t1 (рисунок 115 – для одномерного случая правый конец
свободен). Вместо неопределенной границы первое необходимое условие достижения
экстремума дополняется условием трансверсальности соответственно:
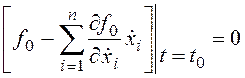
или 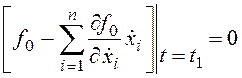 . (24.6)
. (24.6)
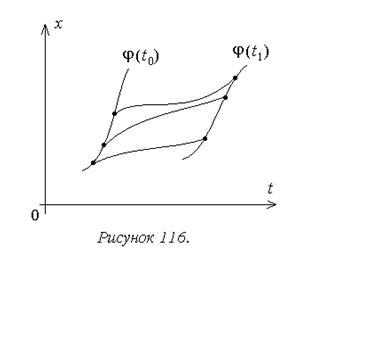 3. Задача со скользящими
концами: вместо значений t0 и x0i заданы уравнения xi(t0)=ji(t0), i=1,2,…,n и аналогично
для правого конца (пример для одномерного случая на рисунке 116). Вместо
условий (24.5), (24.6) вводится условие трансверсальности:
3. Задача со скользящими
концами: вместо значений t0 и x0i заданы уравнения xi(t0)=ji(t0), i=1,2,…,n и аналогично
для правого конца (пример для одномерного случая на рисунке 116). Вместо
условий (24.5), (24.6) вводится условие трансверсальности:
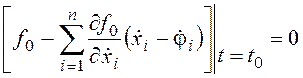
или
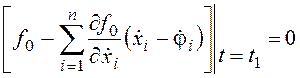 . (24.7)
. (24.7)
Условия трансверсальности используются вместо недостающих граничных условий для нахождения допустимых экстремалей. Отметим еще раз, что количество условий трансверсальности всегда точно совпадает с количеством недостающих в задаче граничных условий. При этом в рассмотренном выше случае 3 уравнения xi(t0)=ji(t0) также рассматриваются как граничные условия и используются для нахождения коэффициентов экстремали вместе с прочими граничными условиями и условиями вида (24.7).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.