Определение автоколебаний нелинейной САУ, страница 2

ДОМАШНЕЕ ЗАДАНИЕ № 4

Определение устойчивости дискретной САУ

Система регулирования имеет в своем контуре цифровую вычислительную машину (ЦВМ). Блок-схема системы с ЦВМ и эквивалентная структурная схема приводятся на рис.2, а и б соответственно.

а)

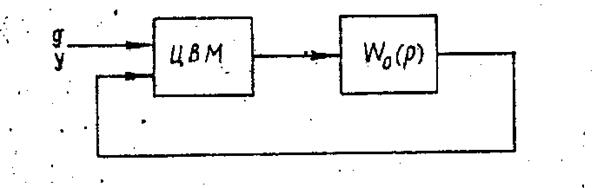
б)

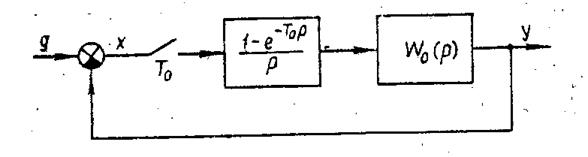                                       Рис.2

Найти Z-передаточные функции разомкнутой W(z) и замкнутой Ф(z) системы в предположении, что запаздывание в ЦВМ отсутствует и можно пренебречь влиянием квантования по уровню, т.е. можно рассматривать линейную задачу. Проверить устойчивость СУ с помощью алгебраического критерия Гурвица и с помощью критерии Найквиста с использованием логарифмических псевдочастотных характеристик.

Рассчитать и представить в виде графика переходную характеристику системы.

Вариант I

Передаточная функция непрерывной части

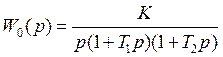
Параметры	Варианты
	1	2	3	4	5	6	7	8	9	10
K, c-1	5,0	5,0	10	10	10	10	10	20	15	15
T1, с	0,1	0,2	0,1	0,1	0,1	0,2	0,2	0,2	1,0	0,8
T2, с	0,02	0,01	0,01	0,02	0,02	0,01	0,02	0,02	0,05	0,04
T0, с	0,04	0,04	0,02	0,02	0,04	0,04	0,01	0,01	0,2	0,15

В таблице К - общий коэффициент усиления, T1, T2 - постоянные времени, T0 - период дискретности ЦВМ.

Вариант II

Передаточная функция непрерывной части:

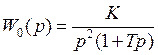
Параметры	Варианты
	I	2	3	4	5	6	7	8	9	10
K, c-2	9	10	10	15	15	20	20	25	25	30
T1, с	0,2	0,14	0,1	0,1	0,08	0,07	0,06	0,05	0,04	0,07
T0, с	0,1	0,1	0,08	0,08	0,05	0,04	0,04	0,03	0,02	0,04

Вариант III

Передаточная функция непрерывной части:

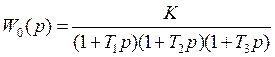
Параметры	Варианты
	1	2	3	4	5	6	7	8	9	10
K, c-1	10	10	15	15	15	20	20	20	25	25
T1, с	3,0	2,5	2,0	1,5	1,2	1,5	1,0	0,8	0,8	0,6
T2, с	1,0	1,0	0,5	0,7	0,8	0,5	0,4	0,3	0,3	0,1
T3, с	0,1	0,1	0,05	0,05	0,05	0,04	0,08	0,06	0,03	0,01
T0, с	0,2	0,2	0,1	0,1	0,1	0,15	0,15	0,12	0,09	0,05

Методические указания

1.  При нахождении W(z) и Ф(z) все предварительные преобразования выполнять в буквенном виде и числовые значения подставлять лишь в окончательно полученные выражения.

2.   Для каждого применяемого критерия устойчивости сформулировать в тексте домашнего задания вывод с кратким обоснованием.

Литература

1.  АндриевскийА.Б., АндриевскийБ.Р., ЕмельяновВ.Ю., КоротковБ.Ф. Теория управления: лабораторный практикум в среде Scilab. – СПб: БГТУ, 2008 (электронная версия).

2.  БесекерскийВ.А., ПоповЕ.П. Теория систем автоматического управления. - СПб: Профессия, изд. 4, 2003.

3.  ЕмельяновВ.Ю. Управление в технических системах: конспект лекций. – СПб: БГТУ (электронная версия), 2008.