Обеспечение экстремума функционала при заданных граничных условиях

Практическое занятие 11. Решение вариационных задач

Пример 1. Требуется обеспечить экстремум функционала 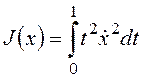 при граничных условиях x(0)=0, x(1)=1.

Найдем частные производные и составим уравнение Эйлера:

, ;

.

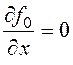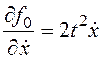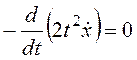После раскрытия скобок здесь будет получено нелинейное дифференциальное уравнение второго порядка. Рационально сразу перейти к интегрированию: , , .

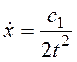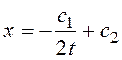Применяя граничные условия, нетрудно убедиться, что допустимой экстремали в данной задаче не существует, то есть задача не имеет решения.

Пример 2. Определить характеристический полином системы автоматического управления, для которой функционал 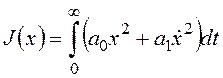 минимален при  a₀,a₁>0 и граничных условиях x(0)=x₀, .

Найдем частные производные и составим уравнение Эйлера:

, ;

.

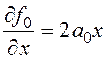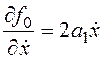Решение полученного уравнения имеет вид: x=c₁e^-at+c₂e^at, где .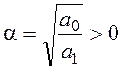

С учетом граничных условий находим c₁=x₀, c₂=0 и допустимую экстремаль в виде: .

Проверим выполнение условия Лежандра: .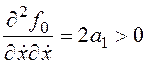

Найденная допустимая экстремаль обеспечивает минимум рассматриваемого функционала и является решением однородного дифференциального уравнения , левая часть которого определяет характеристический полином системы. Здесь он примет вид: D(s)=s+a.

Пример 3. Требуется обеспечить экстремум функционала 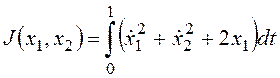 при граничных условиях x₁(0)=1, x₂(0)=0, x₁(1)=3/2, x₂(1)=1.

Найдем частные производные и составим систему уравнений Эйлера-Лагранжа:

, , , ;

,

.

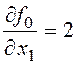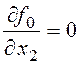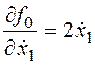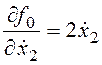Уравнения экстремали: 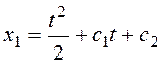, x₂=c₃t+c₄.

С учетом граничных условий находим допустимую экстремаль:

x₁(0)=c₂=1, x₁(1)=1/2+c₁+c₂=3/2, c₁=0, ;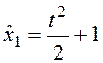

x₂(0)=c₄=0, x₂(1)=c₃+c₄=1, c₃=1, .

Составим матрицу вторых частных производных и проверим выполнение условия Лежандра:

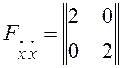,  D₁=2>0, D₂=4>0.

Таким образом, на крив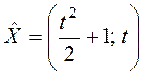ой  обеспечивается минимум величиной .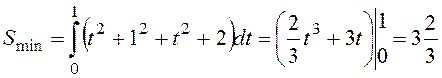

Пример 4. Требуется обеспечить экстремум функционала 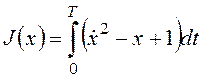 при T>0и граничном условии x(0)=0.

В данной задаче правый конец свободен. Поэтому потребуется составить и учесть для правого конца два условия трансверсальности: одно вида (24.5) и одно вида (24.6).

Найдем частные производные и составим уравнение Эйлера и условия трансверсальности:

, ;

, ;

;

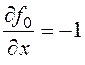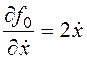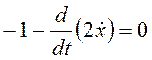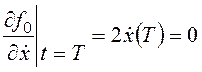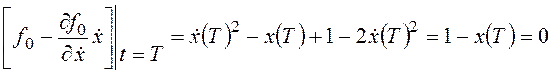 (с учетом ).

Получим уравнение экстремали: 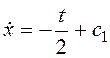, 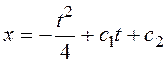. Далее кроме неизвестных констант c₁ и c₂ на основе граничного условия и условий трансверсальности находим также значение T: x(0)=c₂=1, 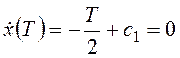, , 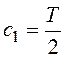, 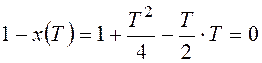T=2, c₁=1, .

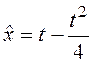Проверим выполнение условия Лежандра: .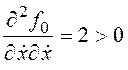

Таким образом, на кривой 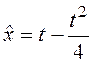 на интервале [0; T] обеспечивается минимум величиной

.

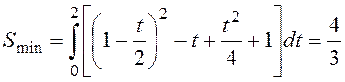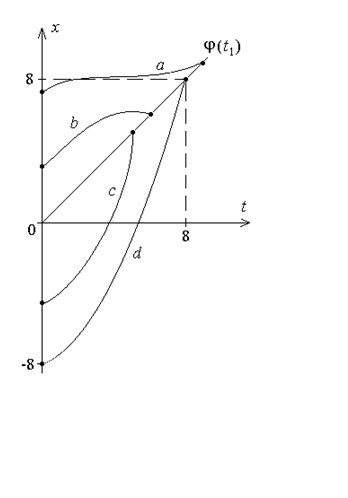Пример 5. Требуется обеспечить экстремум функционала  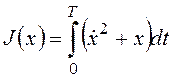при граничном условии x(T)=T, T>0 (рисунок).

В данной задаче левый конец подвижен, правый конец – скользящий по кривой j(T)=T. Поэтому потребуется составить и учесть для левого конца условие трансверсальности вида (24.5), для правого - вида (24.7).

Найдем частные производные и составим уравнение Эйлера и условия трансверсальности:

, ;

, ;

;

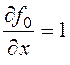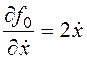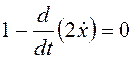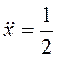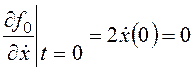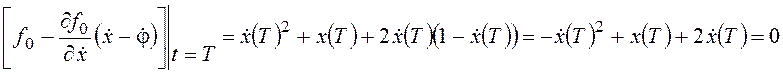
Получим уравнение 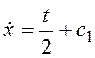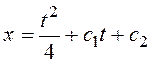экстремали: , . Используем граничное условие и условия трансверсальности для нахождения значения Tи уравнения допустимой экстремали: , , 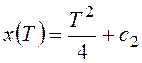, 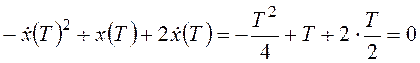T=8, 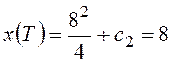, c₂=-8, .

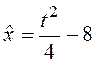Условие Лежандра указывает на минимум.

Таким образом, на кривой 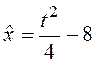 (кривая dна рисунке) обеспечивается минимум величиной .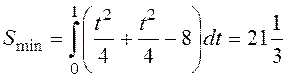

Пример 6.Требуется определить характеристический полином системы управления, для которой функционал 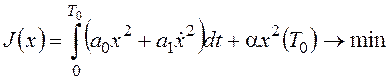. Заданы ненулевое значение x(0)=x₀, положительные a₀, a₁, a, конечное T₀.

Обозначим исходную переменную x=x₁ и введем дополнительную переменную 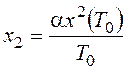, которая на интервале [0;T] является константой. В задаче формально появится одно уравнение связи , а функционал примет вид: .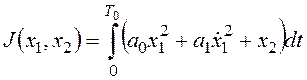

Составим функцию Лагранжа, найдем ее производные, составим уравнения Эйлера-Лагранжа и условие трансверсальности:

;

, , , ;

,

;

.

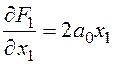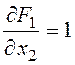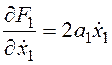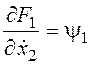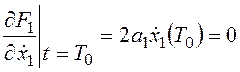Отметим, что поскольку уравнение для x₁ оказалось изолированным, первое дифференциальное уравнение решать не требуется и можно ограничиться только одним условием трансверсальности. Решение последнего уравнения дает общее выражение для выходного сигнала САУ: x=x₁=c₁e^kt+c₂e^-kt, где . Применим граничное условие и условие трансверсальности:

x(0)=c₁e^k0+c₂e^-k0=c₁+c₂=x₀,

.

Таким образом, здесь в отличие от примера 2 обе константы c₁ и c₂ оказываются ненулевыми, в выражении для выходного сигнала содержатся экспоненты как с отрицательным, так и с положительным показателем степени, а характеристический полином системы должен иметь вид: D(s)=(s+k)(s-k).

Отметим, что такая система является асимптотически неустойчивой. Но если работа системы рассматривается на ограниченном интервале времени, работоспособной и, как в рассмотренном примере, оптимальной может быть и неустойчивая с точки зрения классического предельного подхода система.

Пример 7. Требуется обеспечить экстремум функционала 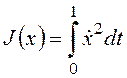 при граничных условиях x(0)=0, x(1)=1 с учетом уравнения связи .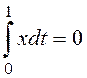

Составим функцию Лагранжа: .

Найдем частные производные и составим уравнение Эйлера (концы в задаче закреплены, условия трансверсальности не требуются):

, ;

.

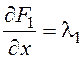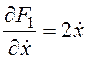Интегрированием уравнения получим: , .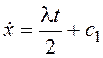

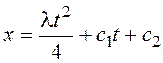Получаемые в изопериметрических задачах уравнения экстремали содержат дополнительные константы – множители Лагранжа. Количество таких констант соответствует количеству уравнений связи, которые и используются вместе с граничными условиями или условиями трансверсальности для нахождения коэффициентов уравнения допустимой экстремали.

Применим граничные условия:

x(0)=c₂=0, x(1)=l/4+c₁=1, l=4-4c₁.

Подставим последнее выражение в уравнение экстремали: x=t²-c₁t²+c₁t, а результат – в уравнение связи:

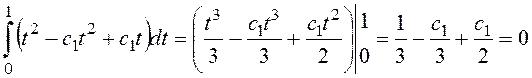, c₁=-2, l=12.

В результате уравнение допустимой экстремали: .

Проверим выполнение условия Лежандра: .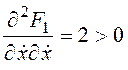

Таким образом, на кривой  обеспечивается минимум величиной .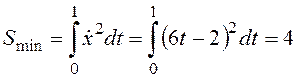

Пример 8. Требуется обеспечить экстремум функционала 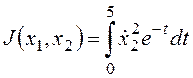 при граничном условии x₂(0)=-2 с учетом уравнений связи , .

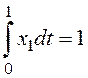Составим функцию Лагранжа: .

Найдем частные производные и составим систему уравнений Эйлера-Лагранжа и необходимые условия трансверсальности (левый конец в задаче частично закреплен, правый подвижен):

, , , ;

,

;

, , .

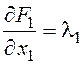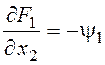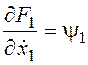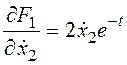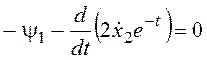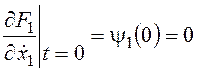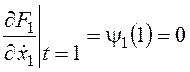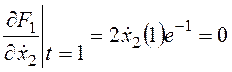Интегрированием полученных уравнений получим: y₁=l₁t+c₁,  .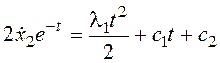

Применив условия трансверсальности, получим c₁=0, l₁=0 c₂=0 и .

Последовательно интегрируя последнее полученное уравнение и уравнение связи, получим уравнения экстремали: x₂=c₃, x₁=c₃t+c₄.

С учетом граничных условий находим допустимую экстремаль: , .

С учетом квадратичной формы интегранта в условиях задачи можно сделать окончательный вывод: на кривой  обеспечивается минимум величиной S_min=0.