Практическое занятие 10. Анализ устойчивости и качества дискретной системы
Пример 1.
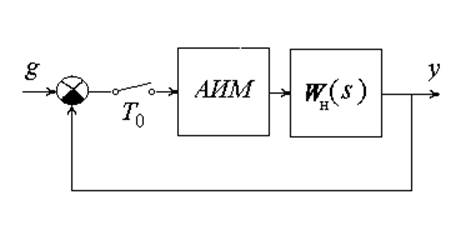
Требуется проанализировать устойчивость замкнутой
системы, с передаточной функцией непрерывной части 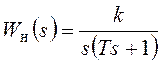 и амплитудно-импульсной
модуляцией. Заданы параметры непрерывной части: k=100c-1, T=0,2c.
Импульсный элемент с тактом величиной T0=0,05с
формирует прямоугольные импульсы. Относительная длительность импульсов
(скважность) g=0,1.
и амплитудно-импульсной
модуляцией. Заданы параметры непрерывной части: k=100c-1, T=0,2c.
Импульсный элемент с тактом величиной T0=0,05с
формирует прямоугольные импульсы. Относительная длительность импульсов
(скважность) g=0,1.
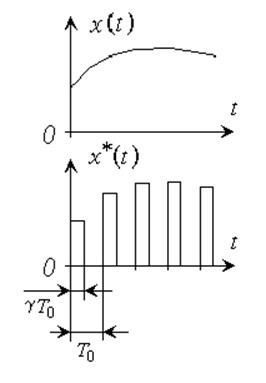
При единичном входном импульсе
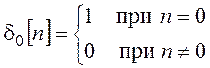
сигнал
на выходе экстраполятора может быть представлен в виде: ![]() .
С учетом его изображения по Лапласу найдем передаточную функцию экстраполятора:
.
С учетом его изображения по Лапласу найдем передаточную функцию экстраполятора:
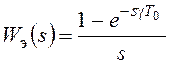 .
.
С учетом gT0<<1 воспользуемся разложением экспоненты в ряд и приближением:
![]() .
.
В результате передаточная функция экстраполятора может быть записана в виде:
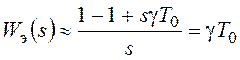 .
.
Передаточная функция непрерывной части с учетом экстраполятора будет иметь вид:
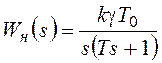 .
.
Дискретная передаточная функция разомкнутой системы в соответствии с таблицей изображений:
|
|
|
|
|
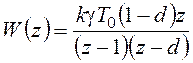 ,
, 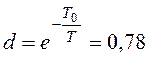 , и
замкнутой системы:
, и
замкнутой системы:
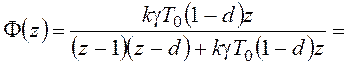
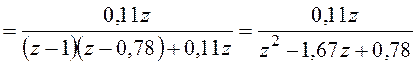 .
.
После подстановки 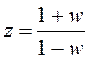 получим
характеристический полином:
получим
характеристический полином:
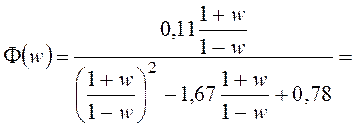
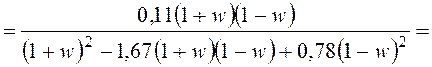
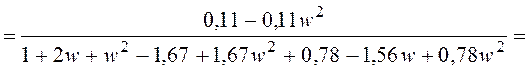
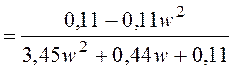 ;
;
![]() .
.
В соответствии с необходимым условием устойчивости данная система второго порядка устойчива.
Для оценки запаса устойчивости воспользуемся частотным методом. Получим передаточную функцию разомкнутой системы
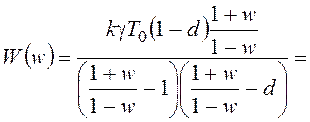
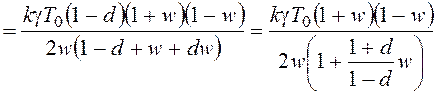 .
.
Подстановкой 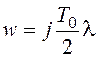 перейдем
к абсолютной псевдочастоте:
перейдем
к абсолютной псевдочастоте:
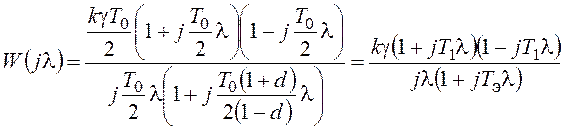 , где
kg=10;
, где
kg=10; 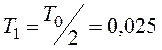 ;
; 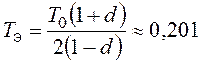 .
.
Получим выражения для логарифмических псевдочастотных характеристик:
![]() ,
,
![]() .
.
Характеристики показаны на рисунке.
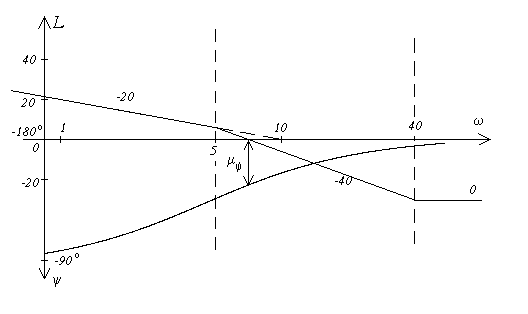
Вывод об устойчивости системы подтверждается. Запас
устойчивости по фазе составляет ![]() .
.
Точность системы в установившемся режиме может быть оценена на основе теоремы о конечном значении.
Установившаяся ошибка от задающего воздействия:
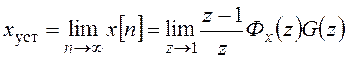 .
.
Найдем передаточную функцию замкнутой системы по ошибке от задающего воздействия для рассматриваемого примера:
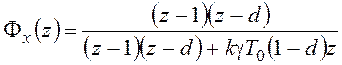 .
.
Для g(t)=g0 1(t)
имеем 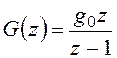 и в результате получим:
и в результате получим:
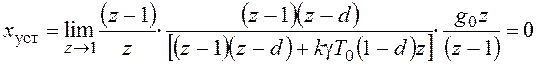 .
.
Данная система обладает астатизмом по задающему воздействию.
Для g(t)=vt1(t) имеем 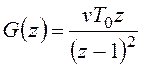 и получим:
и получим:
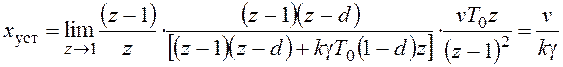 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.