Синтез компьютерного управления

Лекция 21. Синтез компьютерного управления

В общем виде структурную схему системы компьютерного управления можно представить в виде, представленном на рисунке 105.

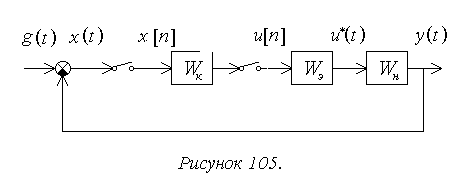
Здесь W_н – передаточная функция непрерывной части системы (объекта управления), W_э – передаточная функция экстраполятора, W_к – дискретная передаточная функция управляющего компьютера. Ключи на входе и выходе компьютера отражают дискретизацию по времени сигнала x[t], вводимого в компьютер, и дискретность формирования управляющего сигнала u[n]. Квантованием по уровню пренебрегаем, предполагая учет его влияния при определении величины коэффициента передачи непрерывной части.

Передаточная функция управляющего компьютера рассматривается в форме отношения z-изображений выходного и входного сигналов:

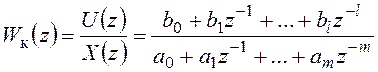.                 (21.1)

От (21.1) можно перейти к разностному уравнению

, которое всегда может быть преобразовано к виду с a₀=1.

Далее выполняется переход к алгоритму формирования сигнала управления u[n]:

.      (21.2)

Как видно из (21.2), для формирования сигнала управления необходимо текущее значение сигнала ошибки, а также l его предыдущих значений и m предыдущих значений сигнала управления. Для их хранения используется оперативная память компьютера.

Требуемая дискретная передаточная функция цифровой части (управляющего компьютера) W_к(z), определяющая алгоритм управления, может быть найдена на основе методов синтеза САУ, разработанных для непрерывных систем.

Если для системы, структура которой соответствует рисунку 105, известна дискретная передаточная функция непрерывной части с экстраполятором W_н-э(z) и найдена желаемая дискретная передаточная функция разомкнутой системы W_ж(z), то передаточная функция цифровой части может быть определена как отношение

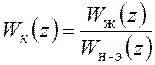.                                          (21.3)

Вместо (21.3) на практике чаще применяется метод синтеза цифровой части на основе частотных характеристик. При этом управляющий компьютер рассматривается как последовательное корректирующее устройство, передаточная функция которого W_к(z)=W_пс(z), может быть найдена через псевдочастотные передаточные функции:

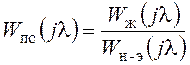,                                       (21.4)

или соответствующие им логарифмические псевдочастотные характеристики:

.                                     (21.5)

Если найдена , далее подстановкам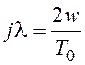и  и 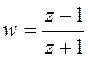 можно перейти к D(z) и алгоритму компьютерного управления.

При использовании соотношений (21.3) - (21.5) следует иметь в виду следующие ограничения:

- степень числителя получаемой передаточной функции цифровой части не должна быть выше степени ее знаменателя (условие физической реализуемости);

- в число нулей и полюсов желаемых передаточных функций системы должны входить все нули и полюсы передаточных функций непрерывной части, лежащие за пределами области устойчивости (условие грубости).

Рассмотрим синтез управляющего алгоритма на примере.

Пусть в системе компьютерного управления с периодом квантования T₀ и экстраполятором нулевого порядка передаточная функция непрерывной части имеет вид:

.

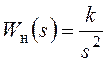Дискретная передаточная функция и частотные характеристики непрерывной части будут иметь вид:

,

,

,

,

.

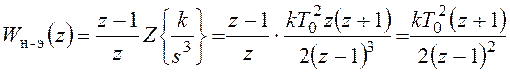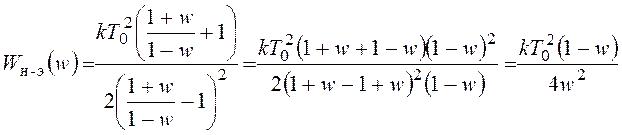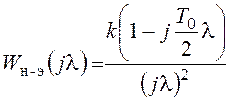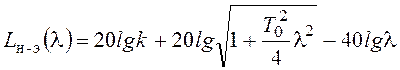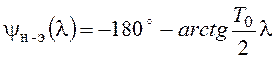Логарифмические псевдочастотные характеристики непрерывной части показаны на рисунке 106а. Ясно, что при простейшем законе управления на основе жесткой отрицательной обратной связи замкнутая система будет неустойчива. Синтез закона управления может быть выполнен аналогично синтезу корректирующего устройства. Выберем желаемую ЛАХ в виде, показанном на рисунке 106а пунктиром. Желаемая дискретная частотная передаточная функция разомкнутой системы с учетом указанных выше требований имеет вид:

,

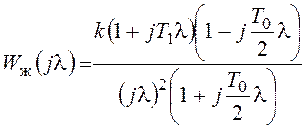а для последовательного корректирующего устройства получим:

.

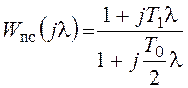ЛАХ последовательного корректирующего устройства показана на рисунке 106б. Требуемое значение T₁ рассчитывается по формуле 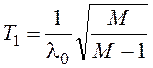, где M – заданное значение показателя колебательности.

Указанными выше подстановками перейдем к дискретной передаточной функции цифровой части:

,

,

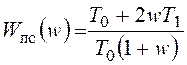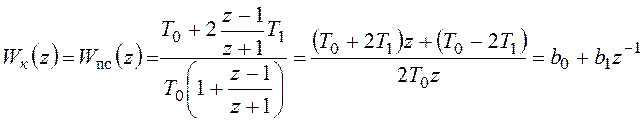где ,  .

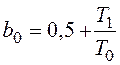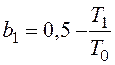В результате получен следующий алгоритм компьютерного управления:

.

Следующий пример показывает важность выполнения условия грубости.

Пусть задана передаточная функция непрерывной части системы компьютерного управления с периодом квантования T₀ и экстраполятором нулевого порядка:

.

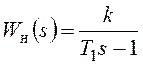Дискретная передаточная функция непрерывной части будет иметь вид:

.

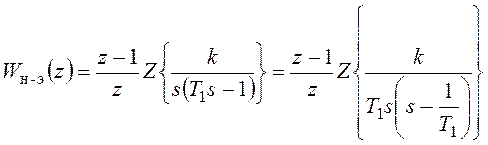Введем обозначения 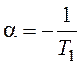 и 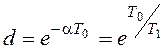, тогда

.

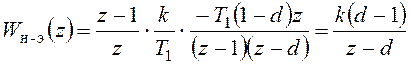Пусть k=2, d=1,2. Тогда

.

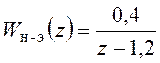Поскольку корень знаменатель (полюс передаточной функции) по модулю превышает единицу, непрерывная часть системы в разомкнутом состоянии неустойчива.

Введем в систему дискретное корректирующее устройство с передаточной функцией:

.

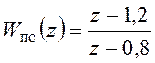В результате получим скорректированную систему с передаточными функциями:

,

.

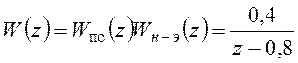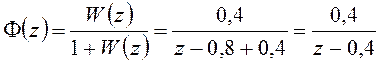Устойчивость замкнутой системы обеспечена за счет того, что «плохой» полюс передаточной функции непрерывной части скомпенсирован «нулем» передаточной функции корректирующего устройства.

Теперь предположим, что за счет погрешностей изготовления отдельных элементов параметры объекта управления будут несколько отличаться от расчетных. Например, примем d=1,201. Тогда изменятся и передаточные функции исходной скорректированной системы:

,

,

.

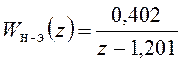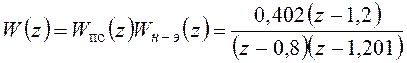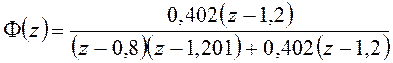Характеристическое уравнение замкнутой системы примет вид:

.

Его корни: 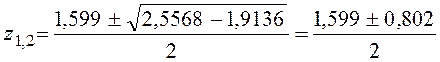, z₁=1,2, z₂=0,399.

Таким образом, при нарушении условия грубости скорректированная система становится неустойчивой даже при незначительном отклонении параметров реальных устройств от расчетных значений.

В таблице 3 приведены некоторые типовые алгоритмы управления и коррекции систем с соответствующими передаточными функциями.

Таблица 3

Тип звена	Непрерывный аналог	Дискретная передаточная функция	Частотная передаточная функция	Алгоритм
Дифференци-рующее		,	,	, ,
Пассивное дифференци-рующее	,	,	,	, , ,
Интегрирую-щее		,
Пассивное интегрирую-щее	,		, ,	, , ,
Интегро- дифференци-рующее		,