Лекция 19. Передаточные функции импульсных звеньев и систем
 Рассмотрим сначала получение
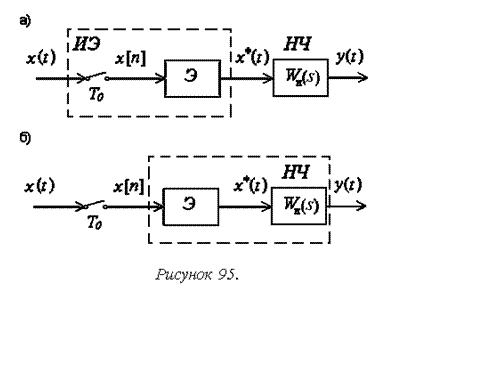
передаточной функции разомкнутой системы (рисунок 95а).
Рассмотрим сначала получение
передаточной функции разомкнутой системы (рисунок 95а).
При получении передаточных функций импульсных систем и звеньев используются два варианта модели импульсного звена – как формирователя решетчатой функции или последовательности d-функций.
Для модели первого вида, в которой сигнал на выходе ключа x[n] рассматривается в форме решетчатой функции, вводится понятие приведенной весовой функции непрерывной части системы. Приведенная весовая функция wп(t) - это реакция непрерывной части на единичную импульсную функцию x[n]=d0[n]. Отметим, что при этом в состав непрерывной части включается экстраполятор (рисунок 95б).
Найдем дискретную передаточную функцию непрерывной части
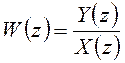 .
.
С учетом ![]() получим:
получим:
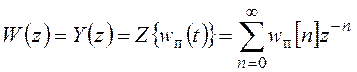 - (19.1)
- (19.1)
результат, аналогичный линейным системам.
Для модели второго вида, в которой сигнал на выходе ключа рассматривается в форме последовательности d-функций:
x[n] = x(t)d(t-nT0), может быть определена обычная непрерывная весовая функция w(t) непрерывной части, включая экстраполятор, как реакция на единичный импульс x[n] = d(t). Далее может быть определена непрерывная передаточная функция непрерывной части
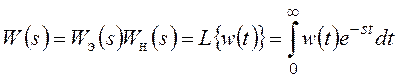 (19.2)
(19.2)
и дискретная передаточная функция непрерывной части
![]() , (19.3)
, (19.3)
совпадающая с (19.1).
 Большинство задач исследования
и проектирования импульсных систем решается с помощью дискретных передаточных
функций, так как при их получении на основе (19.1) или (19.3) полностью
учитываются характеристики импульсной части системы, включая шаг дискретизации
по времени. Однако при использовании импульсных передаточных функций следует
учитывать их некоторые особенности по сравнению с непрерывными, определяемыми
(19.2).
Большинство задач исследования
и проектирования импульсных систем решается с помощью дискретных передаточных
функций, так как при их получении на основе (19.1) или (19.3) полностью
учитываются характеристики импульсной части системы, включая шаг дискретизации
по времени. Однако при использовании импульсных передаточных функций следует
учитывать их некоторые особенности по сравнению с непрерывными, определяемыми
(19.2).
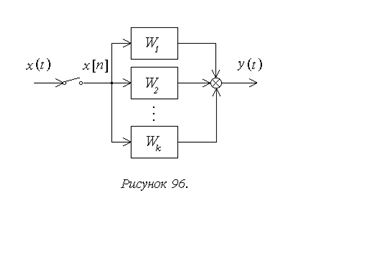
Так при нахождении эквивалентной передаточной функции параллельно соединенных звеньев (рисунок 96) в обоих случаях могут использоваться соотношения:
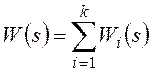 и
и  .
.
В то же время для последовательного соединения при наличии общего ключа на входе (рисунок 97а):
 и
и 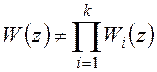 .
(19.4)
.
(19.4)
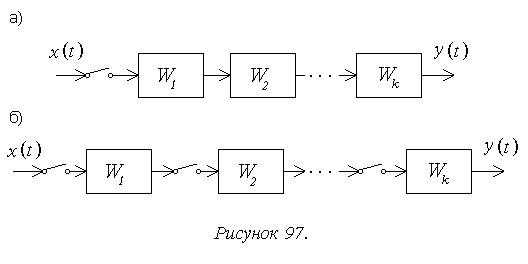
Таким образом, объединение непрерывных последовательно соединенных звеньев и получение общей передаточной функции должно быть выполнено в рамках преобразования Лапласа (19.2) и только потом может быть найдена дискретная передаточная функция всего непрерывного участка системы.
Равенство в (19.4) будет иметь место только при наличии на входе каждого звена своего импульсного элемента (рисунок 97б), причем передаточные функции звеньев и здесь должны определяться совместно с экстраполяторами.
Особенности дискретных передаточных функций проявляются и при описании замкнутых систем.
При наличии единичной отрицательной обратной связи (рисунок 98а) передаточные функции замкнутой системы определяются аналогично непрерывным системам.
Основная передаточная функция замкнутой системы:
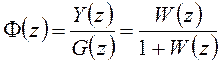 . (19.5)
. (19.5)
Передаточная функция замкнутой системы по ошибке:
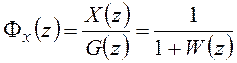 . (19.6)
. (19.6)
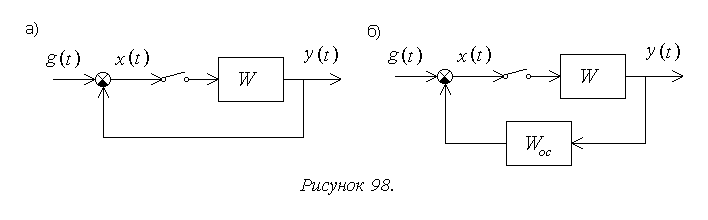
В случае гибкой обратной связи (рисунок 98б) без дополнительного импульсного элемента указанные передаточные функции определяются следующим образом:
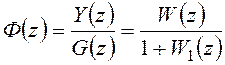 , (19.7)
, (19.7)
где
![]() ,
,
![]() , (19.8)
, (19.8)
Передаточная функция замкнутой системы по возмущению в общем случае может быть получена только при наличии ключа сразу после точки приложения возмущающего воздействия, что на практике встречается редко.
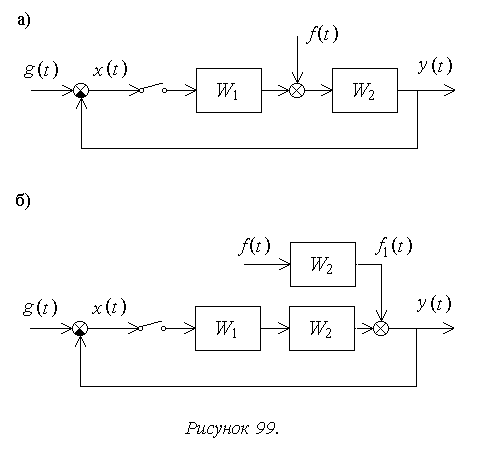
Рассмотрим более распространенный на практике случай, когда возмущающее воздействие f(t) приложено к непрерывной части, как показано на рисунке 99а. Порядок определения реакции системы на возмущение демонстрирует следующий пример.
Преобразуем структурную схему (рисунок 99б) и для сумматора на выходе системы в соответствии с правилом получения передаточных функций дискретных систем при параллельном соединении звеньев получим:
![]() , где
, где
![]() ; F1(z) – z-изображение эквивалентного воздействия f1(t).
Для f1(t) может быть найдено изображение по Лапласу
; F1(z) – z-изображение эквивалентного воздействия f1(t).
Для f1(t) может быть найдено изображение по Лапласу ![]() и далее
и далее ![]() .
.
Теперь учтем, что ![]() ,
причем для рассматриваемой задачи положим G(z)=0:
,
причем для рассматриваемой задачи положим G(z)=0:
![]() , откуда
получим искомый результат:
, откуда
получим искомый результат:
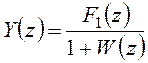 . (19.9)
. (19.9)
При определении передаточной функции непрерывной части ее обычно рассматривают совместно с экстраполятором. При этом экстраполятор стараются строить таким образом, чтобы ослабить влияние эффекта дискретизации по времени на работу системы. Рассмотрим несколько примеров наиболее распространенных экстраполяторов.
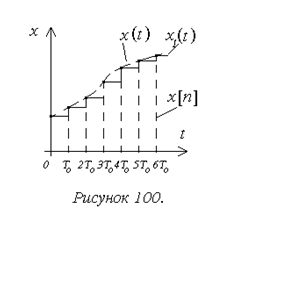 В экстраполяторе нулевого
порядка сигнал на выходе удерживается постоянным в течение всего такта T0(рисунок 100). Здесь x(t) - непрерывный сигнал на входе
ключа, x[n] - решетчатая функция после ключа, работающего с
тактом Т0, x1(t) - выходной сигнал
экстраполятора.
В экстраполяторе нулевого
порядка сигнал на выходе удерживается постоянным в течение всего такта T0(рисунок 100). Здесь x(t) - непрерывный сигнал на входе
ключа, x[n] - решетчатая функция после ключа, работающего с
тактом Т0, x1(t) - выходной сигнал
экстраполятора.
Передаточная функция экстраполятора может быть найдена как изображение по Лапласу его весовой функции, которая имеет вид прямоугольного импульса 1(t)-1(t-T0). Его изображение с учетом теоремы смещения для второго слагаемого:
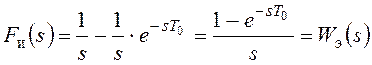 .
.
На основе подстановки ![]() его
можно представить в следующем виде:
его
можно представить в следующем виде:
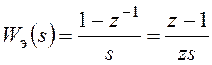 .
.
Тогда передаточная функция приведенной непрерывной части системы с учетом экстраполятора будет равна:
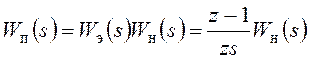 , а
дискретная передаточная функция непрерывной части системы может быть найдена
следующим образом:
, а
дискретная передаточная функция непрерывной части системы может быть найдена
следующим образом:
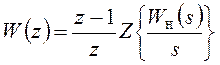 .
.
В экстраполяторе первого порядка сигнал на выходе в течение всего такта изменяется по линейному закону (рисунок 101а):
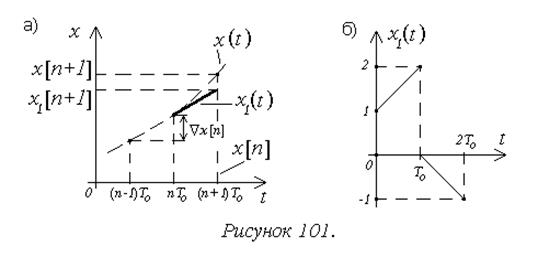
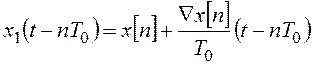 .
.
В результате в конце такта на выходе экстраполятора будет сигнал:
![]() , то
есть здесь также есть погрешность восстановления непрерывного сигнала, хотя и
меньшая, чем в экстраполяторе нулевого порядка.
, то
есть здесь также есть погрешность восстановления непрерывного сигнала, хотя и
меньшая, чем в экстраполяторе нулевого порядка.
Весовая функция экстраполятора первого порядка будет иметь вид, показанный на рисунке 101б:
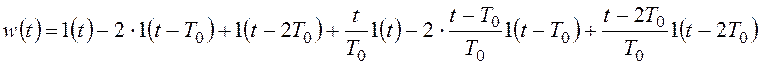 .
.
Найдем ее изображение по Лапласу:
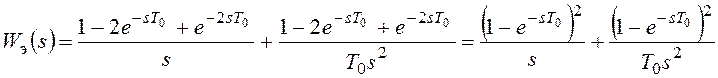 .
.
Выполним
подстановку ![]() :
:
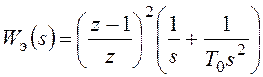 .
.
Теперь дискретная передаточная функция непрерывной части системы может быть найдена следующим образом:
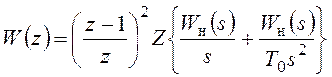 .
.
В рассмотренных выше дискретных экстраполяторах характерной особенностью является сбрасывание накопленной внутри такта ошибки при начале очередного такта. При этом сигнал на выходе экстраполятора в начале очередного такта всегда изменяется скачкообразно. Обеспечить непрерывный выходной сигнал позволяют экстраполяторы, построенные с использованием интегрирующих устройств. Непрерывный экстраполятор первого порядка показан на рисунке 102. Он включает в себя последовательно соединенные экстраполятор нулевого порядка и изодромное звено. Передаточная функция такого экстраполятора будет равна:
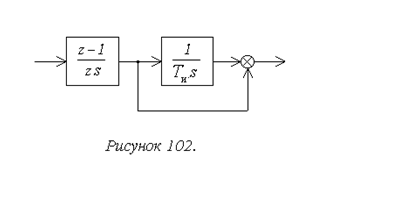
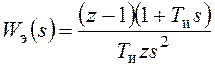 .
.
Дискретная передаточная функция непрерывной части системы в этом случае должна определяться следующим образом:
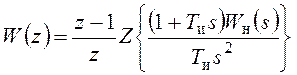 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.