Лекция 5. Алгебраический способ расчета параметров автоколебаний и анализа их устойчивости
 В результате гармонической линеаризации нелинейного звена
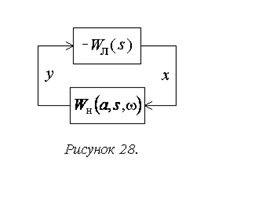
общая структура системы примет вид, показанный на рис. 28, где
В результате гармонической линеаризации нелинейного звена
общая структура системы примет вид, показанный на рис. 28, где
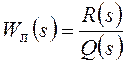 ,
,
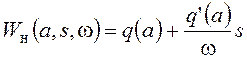
для случая симметричных колебаний. Такой модели соответствует передаточная функция разомкнутой системы
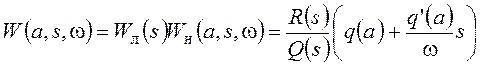
и характеристический полином
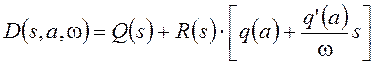 . (5.1)
. (5.1)
После замены s=jw получаем характеристический комплекс:
![]() , на основе которого определяется
периодическое решение x*=a*sinw*t
(симметричные автоколебания) из условия нахождения системы на колебательной
границе устойчивости, получаемого по критерию Михайлова:
, на основе которого определяется
периодическое решение x*=a*sinw*t
(симметричные автоколебания) из условия нахождения системы на колебательной
границе устойчивости, получаемого по критерию Михайлова:
![]() (5.2)
(5.2)
или
![]() (5.3)
(5.3)
Если конечное решение уравнений (5.3) в области положительных вещественных чисел существует, соответствующие значения a* и w* являются параметрами предельного цикла для данной нелинейной системы. Возможны несколько решений и соответственно несколько предельных циклов.
Рассмотрим более подробно порядок решения уравнений (5.3).
Используем представление числителя и знаменателя частотной передаточной функции линейной части системы в алгебраической форме:
![]() ,
,
![]() .
(5.4)
.
(5.4)
После подстановки (5.4) в характеристический комплекс получим:
![]()
![]() .
.
Теперь уравнения (5.3) примут вид:
![]() ,
,
![]() . (5.5)
. (5.5)
Система (5.5) существенно упрощается для однозначной нелинейности, когда q'(a)=0:
![]() ,
,
![]() ;
;
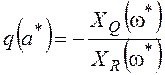 ;
(5.6)
;
(5.6)
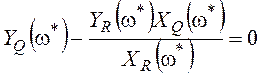 ,
,
![]() . (5.7)
. (5.7)
Уравнение (5.7) позволяет найти частоту предельного цикла. После ее подстановки в (5.6) можно найти и амплитуду.
Для получения условий устойчивости предельного цикла с параметрами a=a* и w=w* учтем, что в переходном процессе, по крайней мере, в малой окрестности предельного цикла, будут иметь место затухающие или расходящиеся колебания, параметры которых будут отличаться от a и w:
![]() . (5.8)
. (5.8)
В символической форме предельному циклу будет соответствовать следующая запись:
![]() , а выражению (5.8):
, а выражению (5.8):
![]() .
.
Следовательно, уравнение (5.2) в окрестности предельного цикла примет вид:
![]() . (5.9)
. (5.9)
Разложим нелинейные функции Xи Y в ряд Тейлора в окрестности параметров предельного цикла, ограничиваясь с учетом малой величины приращений Da и Dw первыми членами разложения. После подстановки разложений в (5.9) получим:
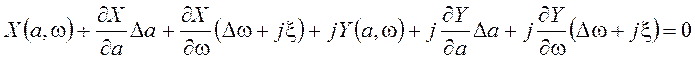 . (5.10)
. (5.10)
Вычтем из уравнения (5.10) уравнение (5.2), соответствующее рассматриваемому предельному циклу, и перегруппируем слагаемые:
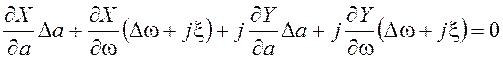 ,
,
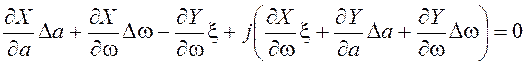 .
.
Последнее уравнение эквивалентно системе двух уравнений:
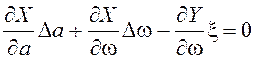 ,
,
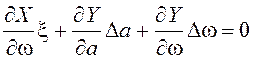 .
.
Исключим Dw из полученной системы:
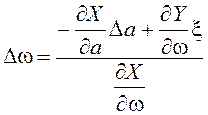 ,
,
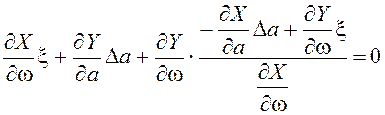 ,
,
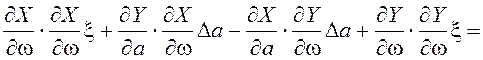
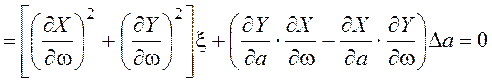 . (5.11)
. (5.11)
Анализ выражения (5.8) показывает, что для устойчивого предельного цикла при Da>0 колебания должны затухать, то есть должно быть x>0, при Da<0 расходиться, x<0. Таким образом, для устойчивого предельного цикла требуется совпадение знаков Da и x, и равенство в (5.11) может быть обеспечено только при выполнении условия
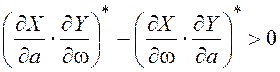 или
или 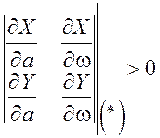 .
(5.12)
.
(5.12)
Символ «*» в (5.12) означает, что данное условие должно выполняться после подстановки в него параметров анализируемого предельного цикла, найденных на основе (5.6)-(5.7), то есть a=a* и w=w*.
Если для найденной пары (a*,w*) условие (5.12) выполняется, остается потребовать, чтобы остальные корни характеристического полинома (5.1), кроме соответствующей рассматриваемому предельному циклу пары чисто мнимых ±jw*, не нарушали устойчивости системы, то есть принадлежали левой полуплоскости. Для проверки этого условия необходим анализ полинома, получаемого путем исключения из (5.1) этой пары корней:
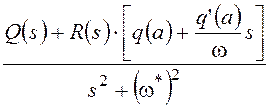 . (5.13)
. (5.13)
Если порядок полинома (5.13) не превышает второго (соответственно, порядок исследуемой системы не превышает четвертого), ограничиваются проверкой необходимого условия устойчивости. При большем порядке к полиному (5.13) следует дополнительно применить критерий Гурвица или Михайлова.
Рассмотрим САУ, структурная схема которой представлена на рис. 29.
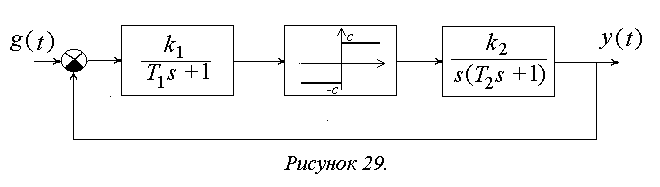
Пусть задающее
воздействие g(t)=0. С учетом
формы статической характеристики нелинейности отметим, что условия
симметричности автоколебаний выполняются. Нелинейность однозначная.
Коэффициенты гармонической линеаризации нелинейности: 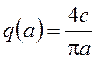 , q’(a)=0.
, q’(a)=0.
Передаточная функция линейной части системы имеет вид:
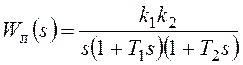 ,
,
![]() ,
, ![]() .
.
Характеристический полином:
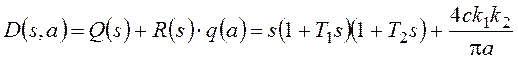 .
.
Составим уравнения (5.6)-(5.7):
![]() ;
;
![]() ,
, ![]() ;
;
![]() ;
;
![]() ,
, ![]() ;
;
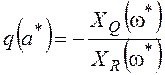 ,
, 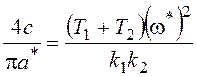 ;
;
![]() ,
, 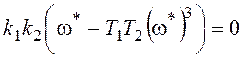 .
.
В результате их решения находим один вариант параметров предельного цикла:
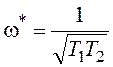 ,
, 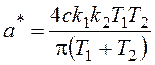 . (5.14)
. (5.14)
Для проверки его устойчивости составим характеристический комплекс системы:
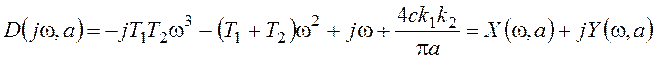 ;
;
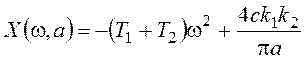 ,
, ![]()
и проверим выполнение условия (5.12):
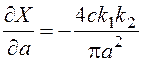 ,
, 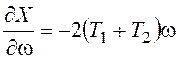 ,
,
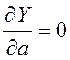 ,
, 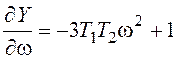 ,
,
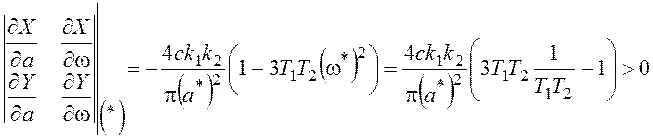 .
.
Поскольку порядок исследуемой системы – третий, можно сделать вывод: в системе будет иметь место автоколебательный процесс с параметрами (5.14).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.