


Лекция 3.Нелинейные системы управления: классификация нелинейностей, особенности процессов в нелинейных системах
Нелинейной называют систему, содержащую хотя бы одно звено, для которого не удается получить или нельзя использовать (в рамках решаемых задач) математическое описание в форме линейного алгебраического или дифференциального уравнения.
Различают нелинейности, или нелинейные звенья, статические и динамические.
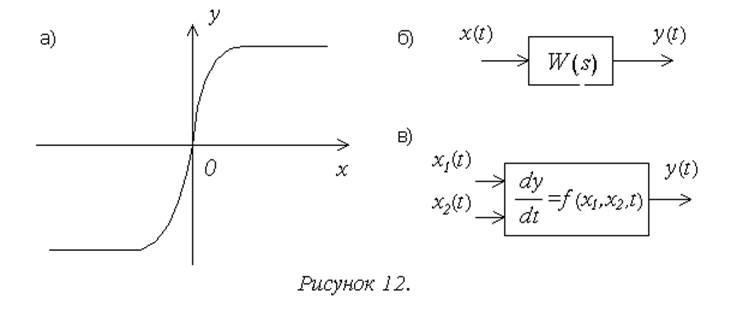
Статическая модель звена не учитывает развития процесса во времени. Общий вид статической модели: Y(t)=f(X(t)) или Y=f(X), где X=(x1,x2,…,xn) – вектор входных переменных (сигналов); Y=(y1,y2,…,ym) – вектор выходных переменных (сигналов) нелинейного звена. Значения составляющих векторов Y и X соответствуют одному и тому же фиксированному моменту времени t. Например, усилитель может быть представлен в математической модели системы нелинейной статической характеристикой (рис. 12,а), позволяющей для любого значения входного сигнала x получить соответствующее значение выходного сигнала y. Такая форма описания предполагает, что входные и выходные переменные могут меняться во времени, но для любого момента времени t значение "выхода" Y(t) зависит только от значения “входа" X(t) в тот же момент времени. Другими словами, статические модели не учитывают предысторию описываемого процесса.
Динамические модели звеньев учитывают развитие процессов во времени, то есть их предысторию. Их общий вид: Y(t)=f({Y(τ),τ<t},{X(τ),τ ≤ t}). Таким образом, значение "выхода" Y здесь может зависеть и от своих значений в предшествующие моменты времени, и от значений "входа" в рассматриваемый и предшествующие моменты времени. Так если рассматривается преобразование усилителем быстро изменяющихся сигналов, приходится учитывать инерционность усилителя, и его модель задается в одной из форм, представленных на рис. 12,б,в.
Методы анализа и синтеза наиболее развиты для систем со статическими нелинейностями. Отсюда и наиболее широкая их классификация. Основные признаки:
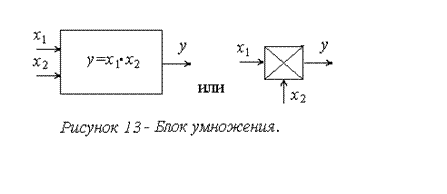
1. С одним (например, рис. 12,а) и несколькими входами (рис. 13).
 |
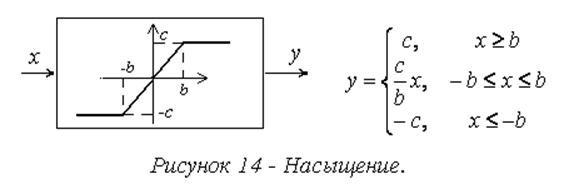
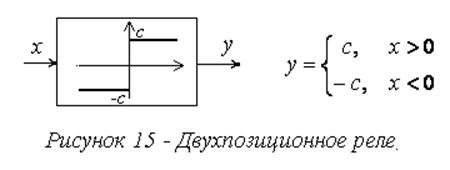
3. Однозначные (рис. 12,а, 13-17),
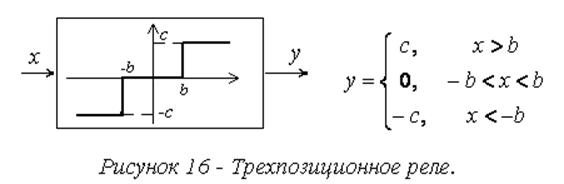
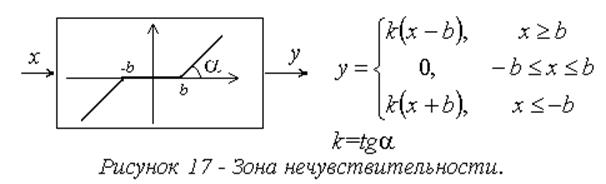
с гистерезисом (рис. 18-19)
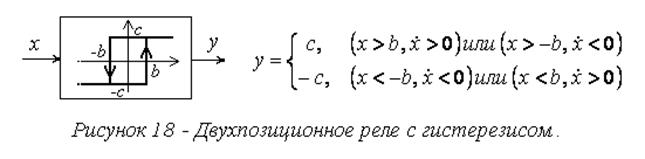
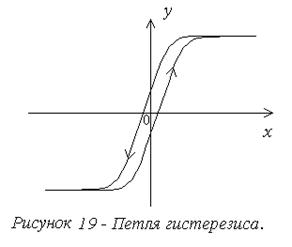
и с опережением (рис. 20).
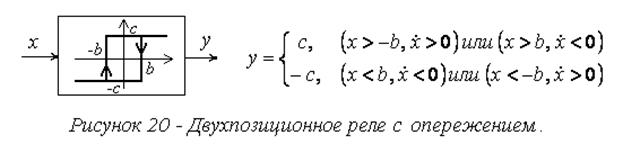
4. Нечетные, y(-x)=-y(x), (рис. 14-20) и остальные, то есть не обладающие свойством нечетности.
Среди основных возможных особенностей процессов в нелинейных системах в первую очередь необходимо отметить следующие.
1. Наличие нескольких состояний равновесия в то время, как у линейной системы состояние равновесия всегда единственное (устойчивое или неустойчивое – в последнем случае оно не достигается и соответственно не наблюдается).
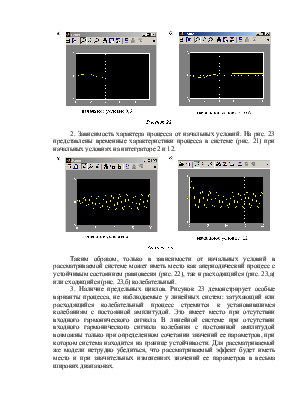
В модели на рис. 21 нелинейное звено – трехпозиционное реле (b=0,5; c=1). При начальных условиях на интеграторе 0,6 и -0,6 в системе достигаются различные устойчивые состояния равновесия (рис.22).
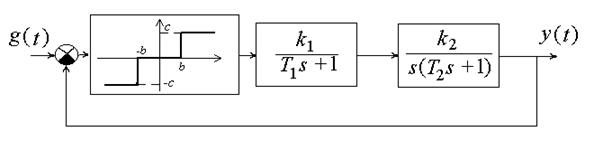
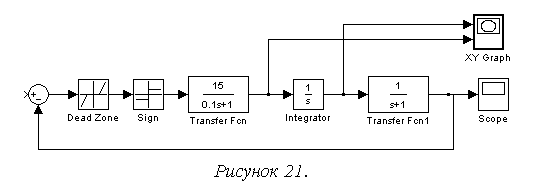
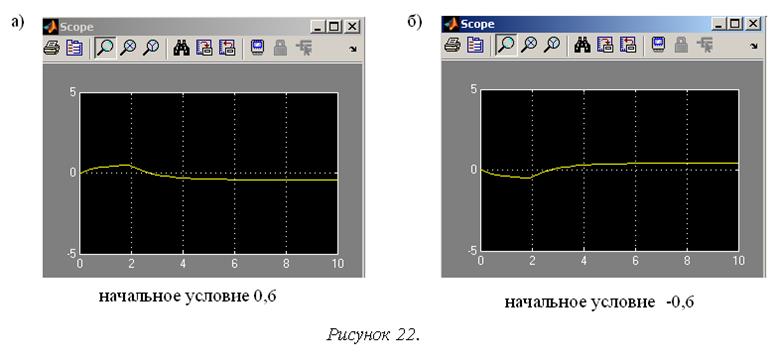
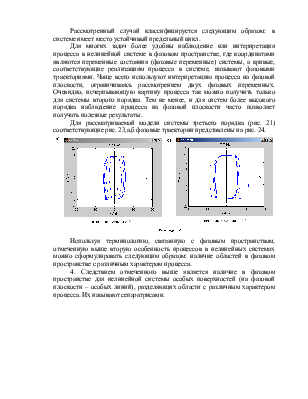
2. Зависимость характера процесса от начальных условий. На рис. 23 представлены временные характеристики процесса в системе (рис. 21) при начальных условиях на интеграторе 2 и 12.
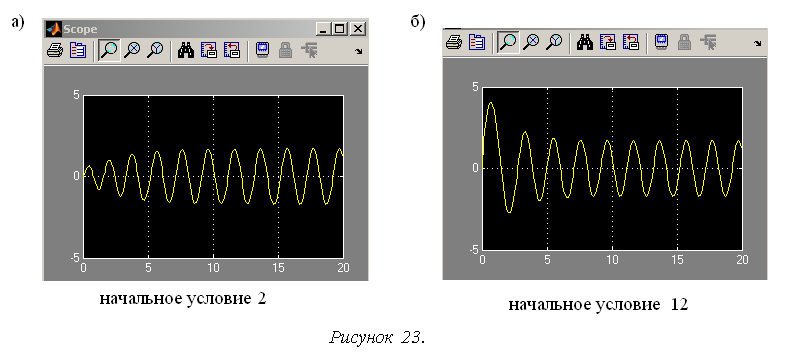
Таким образом, только в зависимости от начальных условий в рассматриваемой системе может иметь место как апериодический процесс с устойчивым состоянием равновесия (рис. 22), так и расходящийся (рис. 23,а) или сходящийся (рис. 23,б) колебательный.
3. Наличие предельных циклов. Рисунок 23 демонстрирует особые варианты процесса, не наблюдаемые у линейных систем: затухающий или расходящийся колебательный процесс стремится к установившимся колебаниям с постоянной амплитудой. Это имеет место при отсутствии входного гармонического сигнала. В линейной системе при отсутствии входного гармонического сигнала колебания с постоянной амплитудой возможны только при определенном сочетании значений ее параметров, при котором система находится на границе устойчивости. Для рассматриваемой же модели нетрудно убедиться, что рассматриваемый эффект будет иметь место и при значительных изменениях значений ее параметров в весьма широких диапазонах.
Рассмотренный случай классифицируется следующим образом: в системе имеет место устойчивый предельный цикл.
Для многих задач более удобны наблюдение или интерпретация процесса в нелинейной системе в фазовом пространстве, где координатами являются переменные состояния (фазовые переменные) системы, а кривые, соответствующие реализациям процесса в системе, называют фазовыми траекториями. Чаще всего используют интерпретацию процесса на фазовой плоскости, ограничиваясь рассмотрением двух фазовых переменных. Очевидно, исчерпывающую картину процесса так можно получить только для системы второго порядка. Тем не менее, и для систем более высокого порядка наблюдение процесса на фазовой плоскости часто позволяет получать полезные результаты.
Для рассматриваемой модели системы третьего порядка (рис. 21) соответствующие рис. 23,а,б фазовые траектории представлены на рис. 24.
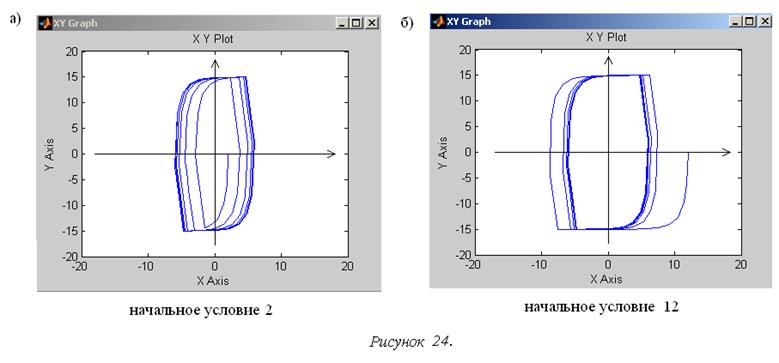
Используя терминологию, связанную с фазовым пространством, отмеченную выше вторую особенность процессов в нелинейных системах можно сформулировать следующим образом: наличие областей в фазовом пространстве с различным характером процесса.
4. Следствием отмеченного выше является наличие в фазовом пространстве для нелинейной системы особых поверхностей (на фазовой плоскости – особых линий), разделяющих области с различным характером процесса. Их называют сепаратрисами.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.