Практический пример применения принципа максимума

Практическое занятие 12. Практический пример применения принципа максимума

Рассмотрим задачу синтеза системы стабилизации, оптимальной по быстродействию.

Рассматривается линейный стационарный объект управления, описываемый системой уравнений , где X – вектор переменных состояния размерности n, U – вектор управляющих сигналов размерности r, Aи B– матрицы постоянных коэффициентов размерности  и  соответственно. Требуется сформировать программу управления и структуру системы, обеспечивающие стабилизацию данного объекта, то есть достижение состояния x_i(T)=0, i=1,2,…,n, за минимальное время. Предполагается наличие начальных условий x_i(0)= x_i0, i=1,2,…,n, и ограничений на управление , l=1,2,…,r.

Как показано в лекции 23, оптимизируемый функционал здесь вводится в виде: .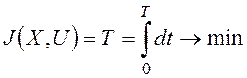

Запишем уравнения объекта управления в развернутом виде и составим функцию Гамильтона:

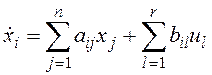, i=1,2,…,n;

.

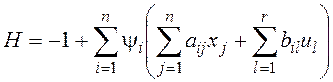Поскольку функция Гамильтона линейна относительно всех аргументов u_i, нетрудно убедиться в отсутствии у нее локального экстремума. Следовательно, оптимальное управление может быть найдено только на границах. Другими словами, каждая составляющая оптимального управления в рассматриваемой задаче может принимать только значения +u_lm или –u_lm.

Перепишем выражение для функции Гамильтона следующим образом:

.

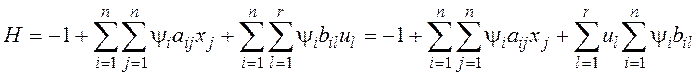Очевидно, что для достижения максимума здесь необходим выбор значений управляющих сигналов по правилу:

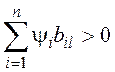  при  ,

  при 

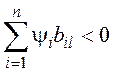
или 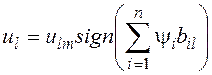, l=1,2,…,r. Такое управление называют релейным.

А.А. Фельдбаумом доказана следующая теорема (теорема об n интервалах): если характеристические числа матрицы A линейного объекта управления вещественные и область допустимых управлений ограничена неравенствами вида , то каждая составляющая оптимального по быстродействию управления кусочно-постоянна и имеет не более n-1 переключения, где n – порядок модели объекта управления.

Итак, при соблюдении условий теоремы в рассматриваемой задаче каждый управляющий сигнал в пределах диапазона времени [0; T] должен принимать значения +u_im или -u_im и сохранять их в пределах интервалов [t_i; t_i+1], причем i=0,1,…,n; t₀=0, t_n=T.

Характеристические (собственные) числа матрицы A могут быть определены путем решения уравнения det(A–lI)=0, где I– единичный вектор размерности n.

Отметим, что результат теоремы распространяется на случай несимметричной относительно начала координат области допустимых управлений: , если только signu_lmax=–signu_lmin.

Для случая комплексных характеристических чисел также доказано, что для линейного объекта, для которого все характеристические числа матрицы A лежат в левой полуплоскости (имеют отрицательную вещественную часть), всегда может быть однозначно определено оптимальное по быстродействию управление, если только границы допустимых значений всех составляющих управляющего сигнала имеют разный знак: signu_lmax=–signu_lmin.

Вернемся к примеру синтеза системы стабилизации искусственного спутника земли относительно продольной оси, рассмотренному в лекции 14. Начальные условия для процесса стабилизации считаются заданными: x₁(0)=x₁₀, x₂(0)=x₂₀ и могут иметь произвольные значения; правые граничные условия нулевые: x₁(T)=x₂(T)=0. Ограничение на управление определяется предельной мощностью двигателей системы ориентации: . Критерий оптимальности управления . Таким образом, получен частный случай рассмотренной выше задачи, в котором объект управления описывается моделью второго порядка (n=2).

Матрица A объекта управления имеет вид: 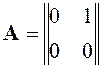, уравнение для определения характеристических чисел 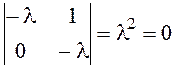, характеристические числа матрицы A l₁=l₂=0 вещественные. Следовательно, в соответствии с теоремой об n интервалах, оптимальный управляющий сигнал на интервале [0; T] может принимать значения +u_m или -u_m, причем возможно не более одного переключения. Возможные варианты:

1) u=u_m, ; 2) u=u_m, ; 3)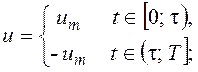

4)

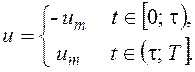
Вид процесса в рассматриваемой системе при двух указанных значениях управляющего сигнала был установлен в лекции 14. Фазовые переменные связаны уравнениями:

при u=+u_m: ;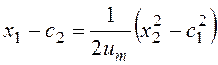

при u=-u_m: 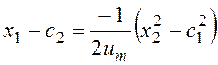, где произвольные постоянные определяются через конкретные начальные условия, а в случае наличия переключения – с учетом условий припасовывания.

При u=+u_m соответствующие фазовые траектории, показанные на рисунке а), будут представлять собой параболы, причем одна из них, уравнение которой

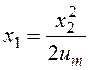, проходит через начало координат. Ее обозначим c⁺.

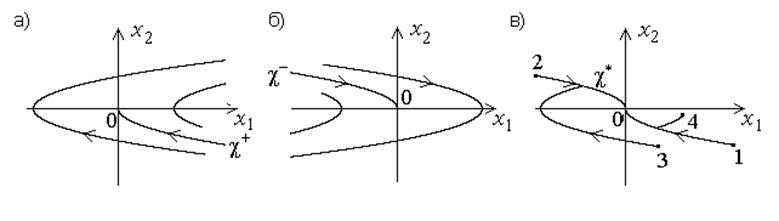
При u=-u_m соответствующие фазовые траектории (рисунок б) также будут иметь вид парабол, причем траектория c^-, проходящая через начало координат, описывается уравнением

.

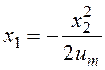Таким образом, достичь требуемого состояния равновесия системы соответствующего началу координат, можно только по траекториям c⁺ и c^-.

Далее с учетом возможности только одного переключения управления в рассматриваемой задаче можно сделать следующие выводы: если точка (x₁₀, x₂₀), соответствующая начальным условиям, будет лежать на кривой c⁺ (правой ветви кривой c^* на рисунке в), оптимальное по быстродействию управление будет иметь вид 1; если точка (x₁₀, x₂₀) окажется на кривой c^- - вид 2; левее кривой c^*, объединяющей c⁺  и c^- - вид 3; правее кривой c^* - вид 4.

В первых двух случаях переключение отсутствует, в последних двух - имеет место одно переключение в момент времени, когда фазовая траектория достигает кривой c^*. Следовательно, кривая c^* является на фазовой плоскости линией переключения для оптимального управления. Уравнение кривой c^* дает условие переключения для оптимального управления:

.

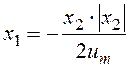Теперь можно записать уравнение оптимального по быстродействию закона управления следующим образом:

.

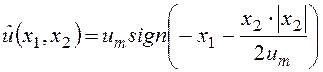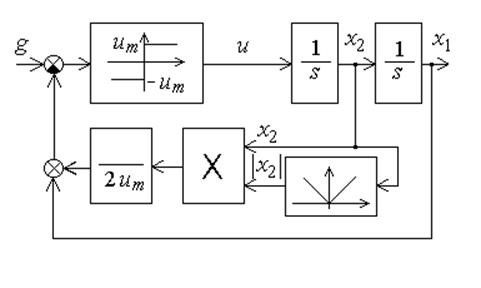
Структурная схема оптимальной по быстродействию системы стабилизации показана на рисунке.