













Глава 7 КАТОДЫ ИОННЫХ ИСТОЧНИКОВ
7.1. Значение выбора катода
Для создания разряда в сильноточных ионных источниках требуются катоды, обеспечивающие ток от сотен до нескольких тысяч ампер. Выбор материала и геометрии таких катодов значительно влияет на многие важные свойства ионного источника, такие, как срок службы, время, необходимое для включения источника, стабильность работы, длительность импульса, подводимая мощность, плотность разрядной плазмы и температура электронов в разряде. Таким образом, очевидна необходимость понимания основных принципов работы катода газоразрядного ионного источника.
7.2. Теория термоэлектронной эмиссии в приближении свободных электронов
Явление термоэлектронной эмиссии многократно описывалось различными авторами [245, 158]. Однако представляется необходимым привести здесь хотя бы некоторые элементарные сведения из теории термоэмиссии.
Термоэлектронная эмиссия представляет собой «испарение» электронов с поверхности твердого тела. Считается, что в проводнике электроны проводимости находятся в плоской потенциальной яме глубиной W (рис. 7.1). Внутри нее электроны подчиняются распределению Ферми—Дирака, т. е. число электронов в единице объема фазового пространства (х, у, z, Рх, Pу, Pz) является функцией энергии
![]() (7.1)
(7.1)
где h — постоянная Планка; εF— величина, называемая энергией Ферми, и
![]() (7.2)
(7.2)
есть кинетическая энергия электрона массой m, который обладает импульсом с компонентами рх, ру, рz. Энергия Ферми определяется из условия нормировки: равенства интеграла по импульсу от функции распределения пространственной плотности электронов в проводнике.
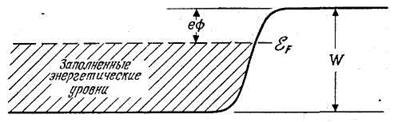
Рис. 7.1. Изменение потенциальной энергии электрона вблизи поверхности металла согласно теории свободных электронов.
импульсу от функции распределения пространственной плотности электронов в проводнике.
При значениях плотности
электронов, характерных для металлов и других проводников, справедливо
соотношение εF>>kT вплоть до
температуры плавления материала. В этом случае распределение Ферми имеет
характерную границу (рис. 7.2): функция практически постоянна до энергии
электронов порядка (εF—3kT) и затем быстро убывает, принимая
значение ![]() при
при![]() . Когда
. Когда ![]() , спад становится чисто экспоненциальным,
как и при классическом распределении Больцмана. Электроны в зоне проводимости
имеют энергию, не превосходящую энергию Ферми, хотя это утверждение абсолютно
справедливо лишь в пределе при
, спад становится чисто экспоненциальным,
как и при классическом распределении Больцмана. Электроны в зоне проводимости
имеют энергию, не превосходящую энергию Ферми, хотя это утверждение абсолютно
справедливо лишь в пределе при ![]() ; когда распределение
Ферми приобретает вид прямоугольника.
; когда распределение
Ферми приобретает вид прямоугольника.
Энергия электрона, находящегося на верхнем из заполненных энергетических уровней (т. е. для которого справедливо ε= ε F), меньше энергии покоящегося электрона, находящегося вне металла, на величину, обозначаемую обычно eΦ и называемую работой выхода.
Предположим, что эмитирующая
поверхность представляет собой плоскость, перпендикулярную оси г. Умножив
выражение (7.1) на скорость ![]() , получим число частиц
из единичного объема пространства импульсов, пересекающих каждую секунду
единицу площади эмитирующей поверхности. Полагая,
, получим число частиц
из единичного объема пространства импульсов, пересекающих каждую секунду
единицу площади эмитирующей поверхности. Полагая,
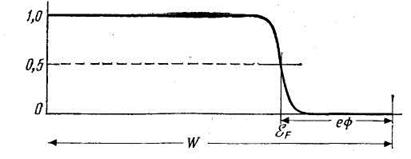
Рис. 7.2. Функция Ферми—Дирака {1+ехр[(е—eF)/kT]}-1 для электронов в зоне проводимости.
![]() что для электронов с большой составляющей
скорости vz нет отражения от поверхности эмиттера внутрь, интегрируя
умноженную на vz и заряд электрона е функцию распределения f(е) по импульсу, получим выражение для плотности тока
эмиссии:
что для электронов с большой составляющей
скорости vz нет отражения от поверхности эмиттера внутрь, интегрируя
умноженную на vz и заряд электрона е функцию распределения f(е) по импульсу, получим выражение для плотности тока
эмиссии:
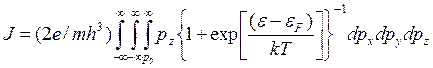 (7.3)
(7.3)
Где ![]() . При
. При ![]() вычисление интеграла
(7.3) приводит к уравнению Ричардсона для плотности тока:
вычисление интеграла
(7.3) приводит к уравнению Ричардсона для плотности тока:
![]() (7.4)
(7.4)
где
![]() (7.5)
(7.5)
есть универсальная константа, равная 1,2*106 А/(м2*К2), или 120 А/(см2*К2).
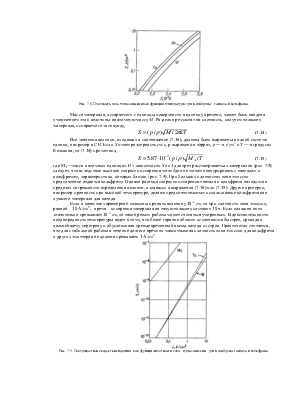
Для подтверждения справедливости
соотношения (7.4) и определения значений констант А и φ величины плотности тока
термоэмиссии измеряются в обширном диапазоне температур и наносятся на график
(рис. 7.3). Линейность полученной зависимости означает, что cправедливо
уравнение Ричардсона — Дэшмана, а наклон линии позволяет найти величину работы
выхода еф. Однако значения коэффициента А, найденные экстраполяцией
графической зависимости ![]() от 1/T к значению при 1/T=0,
как правило, не совпадают с теоретической величиной 120 А/(см2*К2).
Значения коэффициента А для некоторых материалов приведены в табл. 7.1.
от 1/T к значению при 1/T=0,
как правило, не совпадают с теоретической величиной 120 А/(см2*К2).
Значения коэффициента А для некоторых материалов приведены в табл. 7.1.
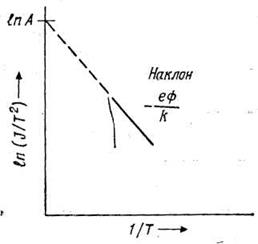
Рис. 7.3. Графическое определение констант ф и А уравнения Ричардсона— Дэшмана.
Хотя величины коэффициента А отличаются от теоретического значения, на справедливость подхода указывает тот факт, что для чистых металлов значения А лежат в -пределах- 0,25—1,33 теоретического значения и существенно отличаются лишь для композитных поверхностей, к которым не применимы столь простые исходные предположения. Полезно упомянуть о допущениях, сделанных при выводе соотношений (7.4) и (7.5), хотя бы и без оценки их справедливости.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.