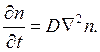
Выражение ![]() Чандрасекар [46] назвал коэффициентом
динамического трения.
Чандрасекар [46] назвал коэффициентом
динамического трения.
Не станем выводить все эти
коэффициенты диффузии, но проиллюстрируем их на одном простом примере рассеяния
электронов на ионах. Здесь главным эффектом является изменение скорости![]() перпендикулярно исходному направлению
движения. Поскольку каждое отклонение происходит в случайном направлении,
имеем задачу случайного блуждания в пространстве скоростей, так что в среднем
квадрат величины
перпендикулярно исходному направлению
движения. Поскольку каждое отклонение происходит в случайном направлении,
имеем задачу случайного блуждания в пространстве скоростей, так что в среднем
квадрат величины ![]() есть сумма квадратов
есть сумма квадратов ![]() , приобретаемых в каждом столкновении. Если
N — число столкновений за секунду, то выражение
, приобретаемых в каждом столкновении. Если
N — число столкновений за секунду, то выражение
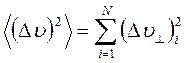 (4.25)
(4.25)
есть искомый коэффициент диффузии. Из рис. 4.2, а следует, что
![]() (4.26)
(4.26)
Однако согласно рис. 4.1 имеем
![]() , так что
, так что
![]() .
.
Из уравнения (4.20) и рис.
4.2,6 получим выражения для![]() и
и ![]() , это дает
, это дает
![]() (4.27)
(4.27)
Число частиц плазмы, для которых параметр столкновений находится в интервале р, p + dp, равно их числу в цилиндрическом слое длиной vс радиусом между р, p + dp, т. е. величине 2πnvpdp, где п — число рассеивающих частиц в единице объема. Суммирование [уравнение (4.25)] приводит к выражению
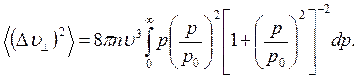
Заменив р/ро на s, получим
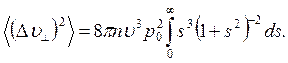 (4.28)
(4.28)
При больших s подынтегральное выражение примерно равно 1/s. Но интеграл от 1/sот любого нижнего предела до бесконечности бесконечен, что явно неприемлемо. Это означало бы, что взаимодействие с далекими частицами столь сильно, что частица, попавшая в плазму, немедленно рассеется на 90°, т. е. вообще не сможет двигаться. Это неправильное заключение меняется, если учесть экранирование.
Используя результаты разд. 4.4, мы неявно предполагали, что любая заряженная частица взаимодействует с любой другой заряженной частицей по закону Кулона и не приняли во внимание эффект экранирования [см. (3.18)]. Можно аппроксимировать экспоненциальный спад потенциала вокруг движущегося заряда, предположив, что внутри сферы радиуса λD экранирование несущественно, а вне этой сферы взаимодействие отсутствует. Учтем это, взяв в качестве .верхнего предела в (4.28) величину
![]() (4.29)
(4.29)
Параметр р0 рассеяния на 90° — величина порядка атомного размера; это приводит к тому, что Λ обычно находится в диапазоне 104—105. При Λ>> 1 имеем
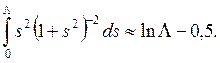 (4.30)
(4.30)
Обычно Λ настолько большая
величина, что![]() ; пренебрегая величиной 0,5 в (4.30),
получим
; пренебрегая величиной 0,5 в (4.30),
получим
![]() (4.31)
(4.31)
Используя ро из (4.21), найдем
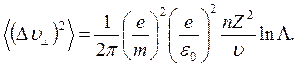 (4.32)
(4.32)
Вычисление дает правильный результат, поскольку интеграл в (4.28) или (4.30) нечувствителен к верхнему пределу. Это означает, что выбор Λ не оказывает влияния на (4.32). Например, типичное значение ln Λ равно 10, что соответствует Λ =22 000. Пусть интеграл обрезан на вдвое меньшей величине, т. е. при Λ = 11 000. Тогда ln Λ станет равным 9,3, т. е. изменится на 7%. В лабораторных условиях почти всегда выбор ln Λ = 10 достаточно точен и дальнейшее вычисление ln Λ обычно не проводится.
Следуя [161], мы вычислили только один из коэффициентов диффузии, и то для особого случая рассеяния электрона на ионах. Полезно иметь результаты и для других случаев. Они получены Чандрасекаром [45, 46] и представлены ниже. В этих соотношениях введены следующие обозначения:
т — масса первичного электрона или иона,
mf— масса полевой или рассеивающей частицы,
Ze— заряд первичной частицы,
Zfe— заряд рассеивающей частицы, а также параметр
![]() (4.33)
(4.33)
равный отношению скорости первичной (рассеиваемой) частицы к корню из среднеквадратичной двумерной скорости рассеивателей. Тогда соотношения Чандрасекара имеют вид
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.