Влияние столкновений. Влияние ионизации на плотность нейтрального газа

Глава 4 ВЛИЯНИЕ СТОЛКНОВЕНИЙ

4.1.  Типы столкновений и общие явления

В гл. 3 была рассмотрена плазма; при этом столкновения совсем не учитывались. Предполагалось наличие ионизации, но возникающее вследствие этого выгорание нейтралов не принималось во внимание. Не учитывались также взаимодействия ионов с атомами и друг с другом по мере их движения к границе. Далее увидим, что упругими столкновениями ионов с атомами действительно можно пренебречь, но столкновения с перезарядкой, при которых ион и атом обмениваются электроном, могут быть существенными.

Для начала отметим, что существуют ограничения на явления, связанные со столкновениями. Из обсужденного в разд. 3.4 критерия Бома следует, что в плазме ионы приходят на границу со средней энергией порядка kT/2. Взаимодействие с нейтральным газом, которое замедляет ионы, должно компенсироваться наличием более сильных полей в плазме вблизи ее границы. Взаимодействие ионов друг с другом не увеличивает их средней скорости движения к границе, но изменяет распределение по скоростям, т. е. будет приводить к максвелловскому распределению относительно средней (дрейфовой) скорости.

4.2.   Влияние ионизации на плотность нейтрального газа

Развитая в разд. 3.5 общая теория Тонкса — Ленгмюра относилась к замкнутой системе, показанной на рис. 3.3. Ионы, достигающие стенок х = ±а, превращаются в атомы и вновь поступают в плазму. Если средняя длина пробега атома до его ионизации больше а, то плотность нейтральных атомов будет сохраняться постоянной, что согласуется с предположением, сделанным при рассмотрении, как указано в разд. 3.7. Если же эта длина мала по сравнению с а, то плотность газа и скорость ионизации будут значительно выше у стенок, чем в центре плазмы.

Конфигурации ионных источников    весьма разнообразны и обычно используют магнитные поля, но сейчас будем считать, что в источнике имеется плазма плоской геометрии, как показано на рис. 3.3, однако стенки перфорированы с целью извлечения ионов. Поток ионов и нейтральных атомов сквозь отверстия перфорации должен быть компенсирован наличием источника нейтралов, например в медианной плоскости х=0. При этом если средний пробег атома до ионизации <<Са, то будем иметь пик в распределении п_а при х = 0 и возрастание п_а на границах вследствие соударений ионов с перемычками на перфорированных стенках.

Оценим среднюю длину пробега. Если ионизация производится максвелловскими электронами, то среднее время существования атома до того, как он ионизуется, задается выражением

                                                                             (4.1)

где п_е—плотность электронов, a — среднее значение произведения сечения ионизации на скорость электрона, изображенное на рис. 3.17. Удаление иона от плоскости за это время равно

                                                     (4.2)

где Т_а — температура нейтрального газа. Из рис. 3.17 для ртутной плазмы при kT_e = 4 эВ получим  = 8,4∙10 ^-15 м³/с. Если kT_а = 0,05эВ (580 К), то

где х_а выражена в метрах, а п_е — в электронах в кубическом метре. Если n_е = 5∙10¹⁷ м ^-3, что является для плазмы ионных источников весьма умеренной величиной, то х_а = 3,7 см; это значение не согласуется с предположением об однородном распределении п_а в источниках, размеры которых велики по сравнению с 3,7 см.

Эффективная длина «гибели» нейтрального атома должна возрастать вследствие эффекта перезарядки, которая эффективно убыстряет движение нейтралов по мере ускорения ионов. Этот эффект обсудим в следующем разделе.

Здесь не предполагается рассматривать плазму с реально существующими пространственными вариациями плотности нейтральных атомов. Это — интересная задача, поэтому читателям предлагается провести следующий расчет. Предположим, что для случая, показанного на рис. 3.3, атомы поступают в объем с медианной плоскости со скоростью βJ_i и с границы х = ±а со скоростью (1—β)J_i, где β — доля извлекаемого с границы тока, формирующая ионный пучок. Принимая во внимание выгорание нейтралов вследствие ионизации и наличие перезарядки при столкновении атомов с ионами, попробуйте найти V(x), плотность ионного тока и поток нейтральных атомов из объема плазмы. Эта задача не решается аналитически, и следует провести численный расчет.

4.3. Столкновения ионов с атомами

Если ионы в плазме движутся к границам со скоростями, которые существенно выше скоростей атомов, то средняя длина пробега между столкновениями с атомами задается выражением

                                                                 (4.3)

где п_а — плотность атомов, — сечение столкновения иона с атомом. Несмотря на то, что было сказано в разд. 4.2, возьмем п_а из (3.67) и получим следующее выражение для случая ионизации максвелловскими электронами:

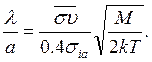                                                             (4.4)

Если же ионизация идет за счет первичных электронов с энергией eV, для которых сечение ионизации равно σ_p, то с учетом (3.71) можно записать

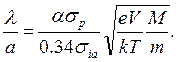                                                        (4.5)