Влияние столкновений. Влияние ионизации на плотность нейтрального газа, страница 3

m₁r₁ = m₂r₂                                                                                               (4.8)

и

                                                         (4.9)

где  и — скорости частиц, когда они находятся далеко друг от друга, а r₁и r₂ — расстояния от начала координат, на которых они находятся. Из сохранения момента импульса следует, что

                         (4.10)

где р₁ и р₂ — прицельные расстояния частиц (рис. 4.1), а угол отсчитывается от оси у, проходящей через точки наибольшего сближения частиц. Подставив (4.8) в (4.10) и положив р₁+ р₂ = р, получим соотношение

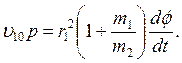                                                                   (4.11)

Расстояние р называется    параметром    столкновения. Из диаграммы в верхнем правом углу    рис. 4.1, показывающей начальный и конечный импульсы частицы 1, можно видеть, что изменение импульса равно

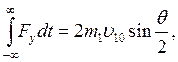                                                           (4.12)

где θ — угол   рассеяния.   Но   F_y=Fcos,   где   F— кулоновская сила, так что

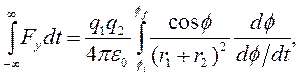                                            (4.13)

где _iи _f— начальное и  конечное значения угла   . Используя выражение (4.8), получим

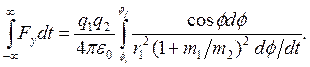
Если теперь учесть (4.11), то имеем

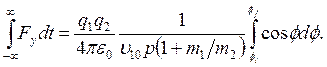
Поскольку ,   можно   записать   следующее   выражение:

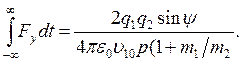                                           (4.14)

Ho  так что из (4.12) и (4.14) получим уравнение

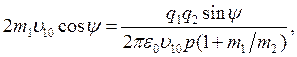
которое можно записать в виде

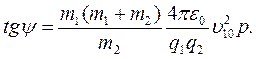                                                   (4.15)

Легко показать, что (4.9) эквивалентно выражению

где

                                                                     (4.16)

есть относительная  скорость     частиц.  Если  подставить ее  в (4.15), то получим

                                                      (4.17)

где (μ — приведенная масса, равная

μ= m₁m₂/(m₁ + m₂).                                                               (4.18)

При рассеянии на угол 0 = 90° угол ψ= 45° и из (4.17) найдем параметр рассеяния

                                                          (4.19)

Уравнение (4.17) можно записать в виде

                                                                        (4.20)

При столкновении электрона с ионом можно подставить электронную массу вместо приведенной, и параметр р₀ рассеяния на 90° запишем в виде

                                                             (4.21)

где Ze— заряд иона. Заменив энергию электрона на величину eV_e, получим из (4.21)

                                                            (4.22)

Сечение рассеяния на угол  равно

Если плотность рассеивателей есть п, то свободный пробег между столкновениями с рассеянием на 90^е равен

                                                          (4.23)

а среднее время между столкновениями составляет

                                                         (4.24)

Заметим, что для малых θ угол ψблизок к π/2; из (4.20) следует, что  при. В дальнейшем будет показано, что суммарный эффект от далеких столкновений на малые случайные углы превалирует над эффектом от близких столкновений. Для того чтобы показать это, необходимо провести статистическое рассмотрение.

4.5. Рассеяние в плазме

Если в плазме движется поток заряженных частиц, то парные столкновения этих частиц с ионами и электронами плазмы могут быть описаны тремя параметрами, которые называются коэффициентами диффузии. Эти три параметра, которые обозначим соответственно ,  и , дают среднее изменение за секунду компоненты скорости в направлении движения, среднее изменение за секунду квадрата этой компоненты скорости и среднее изменение за секунду квадрата компоненты скорости перпендикулярно направлению движения. Последние два параметра описывают диффузию в пространстве скоростей аналогично константе Dв обычном уравнении диффузии