Упругие столкновения электронов и ионов с атомами

Упругие столкновения электронов и ионов с атомами

1. Зависимость сечения упругого рассеяния электронов от энергии. Эффект Рамзауэра.

2. Потеря импульса и энергии электрона при упругом рассеянии

3. Упругое рассеяние ионов. Поляризационное взаимодействие и резонансная перезарядка

4. Потеря направленного импульса и энергии ионом

1. Сечение упругого рассеяния электрона на атомах

До настоящего времени нет никаких экспериментов, свидетельствующих о наличии внутренней структуры электрона. Т.о. на современном уровне развития науки электрон является истинно точечной частицей. Тогда исходя из модели твердых шаров следует ожидать, что эффективное сечение рассеяния электрона на атоме будет равно площади поперечного сечения атома pd²/4. Для наиболее широко используемого в различных экспериментах газа аргона d = 3.58×10^-8см и для сечения получается ~ 10^-15 см² . Эта цифра вполне может служить для проведения оценок по порядку величины, но конечно на самом деле процесс взаимодействия электрона с атомом существенно более сложнее, чем столкновение двух биллиардных шаров и с изменением скорости или энергии налетающего электрона сечение ведет себя достаточно сложным образом. Но прежде чем обсуждать это поведение сделаем еще одну оценку. Оценим де-бройлевскую длину волны для электрона, обладающего характерной для газовых разрядов энергией 1 эв. Скорость, соответствующая этой энергии равна 6×10⁷см/сек, а

 = 1.05×10^-27эрг×сек/(9.1×10^-28гр×6×10⁷см/сек) ~ 2×10^-8см.

Т.о. де-бройлевская длина волны сравнима с размерами атомов и процесс рассеяния электрона на атоме не может быть описан в рамках классической механики. Необходимо рассмотрение с использованием подходов квантовой механики. Именно квантовомеханическими эффектами объясняется наличие глубокого минимума на зависимости s(e) при энергиях в десятые доли электронвольта, наблюдаемого как для аргона, так и для ряда других газов. Наличие этого минимума называется эффектом Рамзауэра, по имени физика впервые обнаружившего его экспериментальным путем. Правда следует отметить, что в некоторых книгах говорят не о Рамзауэровском минимуме, а о Рамзауэровском максимуме, имея ввиду увеличение сечения при еще меньших энергиях (при e®0). С увеличением же энергии сечение нарастает и при e ~12 эв достигает максимума  ~  2×10^-15 см² , т.е. в 2 раза больше чем проведенная оценка, и наконец после этого наблюдается монотонное уменьшение величины упругого сечения. Для ряда газов зависимость сечения от энергии имеет похожий вид, для других довольно заметно отличается, например отсутствует Рамзауэровский минимум. В области больших энергий для всех газов сечение монотонно уменьшается.

2. Потери импульса и энергии электронов при упругом рассеянии.

В результате столкновения электрон может рассеятся самым различным образом, причем вероятность рассеяния на тот или иной угол определяется, как мы уже знаем, величиной дифференциального сечения ds/dW. Зависимость ds/dW от угла также имеет достаточно сложный вид, но все же можно сказать, что при небольших энергиях рассеяние близко к изотропному, т.е. вероятности рассеяния на различные углы примерно одинаковы, а с увеличением энергии происходит увеличение доли частиц рассеянных на малые углы. Очевидно, что в первом случае ансамбль налетающих частиц полностью утратит направленное движение после того как частицы испытают по столкновению, а во втором до определенной степени сохранит его. Поскольку ток это направленное движение заряженных частиц, то для физики газового разряда это имеет существенное значение.

Давайте обсудим потерю направленного импульса более подробно. Но прежде покажем, что при упругом взимодействии электрона с атомом, скорость электрона практически не уменьшается. Рассмотрим лобовое столкновение при котором передача энергии максимальна. Запишем законы сохранения импульса и энергии:

,                                                                     (1)

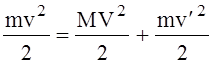.                                                            (2)

где - масса электрона, его скорости до и после столкновения, - масса атома, - его скорость после столкновения. До столкновения атом считаем покоящимся. Из (1) получим

                                                                  (3)

Подставляя (3) в (2) получаем

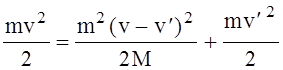                                                      (4)

Сокращая на  и перенося  в левую часть получаем

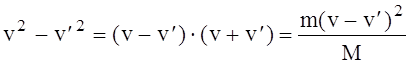                                  (5)

Сокращаем на  и группируем члены содержащие слева, а  справа.

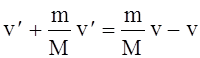.                                                                     (6)

Окончательно для  получаем

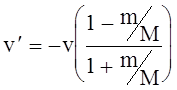                                                                           (7)

Из полученного выражения видно, что скорость поменяет направление, но по модулю практически не изменится, так как входящее в числитель и знаменатель отношение  является величиной много меньше единицы, напрмер для атома аргона  10^-5. Ясно, что при касательном столкновении передача энергии и изменение модуля скорости электрона будут ещё меньше. Соответственно можно сказать, что практически не измениться и модуль импульса частицы.

Пусть импульс электрона равен р до столкновения и р¢ после столкновения. Разложим р' на две составляющие параллельную и перпендикулярную первоначальному направлению движению. Очевидно, что при усреднении по всем возможным углам перпендикулярная составляющая даст нулевой вклад, а усредненная величина параллельной составляющей определит степень сохранения направленного движения. Потеря направленного импульса Dр_|| определится следующим соотношением

Dр_||= р'×соsq×е_р - р = -р(1-р'соsqр)  -р(1-соsq)                          (8)