Упругие столкновения электронов и ионов с атомами, страница 2

Усредняя по всем возможным углам получим

Dр = D + Dр_|| = 0 - р(1- соsq)                                 (9)

При изотропном рассеянии <соsq>=0 и получается что частицы после только одного столкновения полностью утрачивают направленное движение. Если же преобладает рассеяние на малые углы, то <соsq> близок к 1 и получается, что теряется лишь малая часть направленного импульса, а для полной потери необходимо испытать несколько столкновений.

Теперь предположим, что некоторая сила вновь и вновь сообщает электрону направленный импульс р после каждого испытанного столкновения. Тогда за время dt электрон испытает ndt столкновений и полное изменение импульса за это время за счет столкновений

dр = -р(1-<соsq>)ndt = -рn_эфdt                                                 (10)

Поделив на dt получим потерю импульса за единицу времени

dрdt = -рn_эф.                                                                                                                 (11)

Вспоминая закон Ньютона

dp/dt = F                                                                                  (12)

и сравнивая его с полученным выражением получаем, что направленному движению электрона, имеющего импульс р, сквозь газ как бы препятствует некая сила трения

F_тр = - n_эфр                                                                               (13)

пропорциональная эффективной частоте столкновений, а значит транспортному сечению.

Теперь обсудим вопрос о потере энергии при столкновениях. Если импульс электрона при столкновении с атомом изменился на Dр, то соответственно на такую же величину изменился импульс атома. И если принять что до столкновения атом покоился и имел нулевые импульс и энергию то после столкновения он будет иметь импульс Dр и энергию

.                                                             (14)

Соответственно такую же энергию потеряет электрон за одно столкновение, а за время dt  испытав ndt столкновений он потеряет

d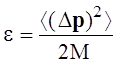ndt                                                         (15)

Вычисляя

<(Dр)²> = <р'² -2р'рсоsq + р²> 2р²(1-<соsq>) =

= 4me(1 - <соsq>)                                                             (16)

и подставляя полученное соотношение в (15) получаем

de/dt = - 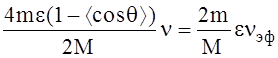                (17)

Нетрудно видеть, что передача энергии от электронов атомам идет крайне медленно так как m/M очень малая величина и поэтому как правило в разрядах электроны, получающие энергию от электрического поля, имеют температуру заметно превышающую температуру газа. Исключением являются дуги высокого давления так как при высоких давлениях велика частота столкновений. Отметим также, что потеря энергии, как и потеря импульса пропорциональна эффективной частоте столкновений, связанной с транспортным сечением.

Следует обратить внимание на один нюанс: В определении транспортного сечения фигурирует угол c - угол рассеяния в Ц-системе. В вышеприведенных формулах фигурирует угол q, так принято обозначать угол рассеяния в Л-системе. Но для рассмотренного случая рассеяния электрона на атоме Ц и Л системы, и, соответственно, углы q и c практически совпадают, что обсуждалось на предыдущей лекции. Поэтому замена произведения n(1- на n_эф вполне правомерна.

3. Упругое рассеяние ионов на атомах.

В отличие от электрон-атомного взаимодействия процесс упругого рассеяния ионов на атомах вполне может быть описан с использованием классической механики. Длина волны Де-Бройля например для иона аргона при e = 1 эв, что соответствует скорости v = 2.16×10⁵ см/с, составляет Мv = 8.76×10^-11 см, что существенно меньше размера атома 3.58×10^-8 см. Тем не менее это взаимодействие также происходит существенно более сложным образом, чем взаимодействие двух твердых шаров. Долгое время считалось, что взаимодействие иона с атомом имеет так называемый поляризационный характер. Ион своим зарядом отталкивает положительно заряженное ядро и притягивает электроны, входящие в состав атома. В результате атом приобретает дипольный момент, пропорциональный напряженности электрического поля иона