Термостимулированная люминесценция твердых тел: Учебное пособие, страница 5

Связь между температурой Т_m, соответствующей максимальному значению интенсивности люминесценции, и значениями β, ε, ν можно вывести из приведенных уравнений.

Из формул (2.1) и (2.6) получаем

I = nν exp (—ε/kT).(2.9)

Для температуры Т = T_m должно быть dI/dT = 0. Продифференцируем уравнение (2.9):

 .

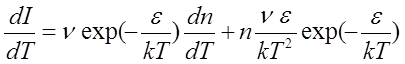Приравнивая производную нулю, получаем

.                                                                                (2.10)

Учитывая, что dt = dt/β, из формулы (2.5) получаем

.                                                                       (2.11)

Подставив значение (dn/n)_T=Tm из формулы (2.11) в (2.10), после простых преобразований получим искомое соотношение

 .                                                                             (2.12)

Способы определения параметров ловушек (центров захвата)

В реальной ситуации формула (2.12) может оказаться неприменимой. При определенных экспериментальных условиях справедливо приближенное эмпирическое соотношение ε=25 kT_m .

Заметим, что полученное выражение (2.7) определяет интенсивность ТСЛ лишь в случае мономолекулярного процесса. В общем случае кинетика процесса ТСЛ является немономолекулярной и описывается уравнением

                                   (2.13)

где m – показатель кинетики процесса ТСЛ (m =1 – мономолекулярный процесс, m=2 – бимолекулярный). В  частности, для бимолекулярного процесса, когда вероятность повторного захвата электронов ловушками гораздо больше вероятности рекомбинаций, затухание свечения будет происходить более медленно по законам бимолекулярной кинетики, т.е. пропорционально квадрату концентрации возбужденных центров.

Для конкретного типа центров захвата порядок кинетики процесса термолюминесценции может быть определен по форме пика ТСЛ. В отсутствие повторного захвата электронов быстрый распад ловушек определенного сорта приведет к более крутому спаду высокотемпературной части максимума спектра ТСЛ. При повторном захвате освобожденных электронов ловушки опустошаются более медленно, что приводит к более пологому спаду высокотемпературной части максимума ТСЛ. Установлено, если 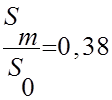    ,   то m = 1,               если   =0,52,      то m=2,                где S_m – площадь пика со стороны высоких температур; S₀ – общая площадь пика ТСЛ (рис.6).

Существует ряд методов определения параметров центров захвата. Часть методов использует отдельные элементы кривой ТСЛ, другие – всю кривую, и имеют в связи с этим различную степень точности.

В методе Урбаха используется спадающая часть пика ТСЛ. Глубина ловушки e определяется так:

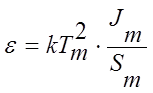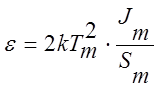     при  m = 1,               при  m=2              (2.14)

где S_m=S₀^.d₀/d_m, где  S₀,  d₀, d_m – соответственно площадь под пиком, ширина и полуширина пика на полувысоте (рис.6), при этом d_m = (T₂-T_m), d₀ = (T₂-T₁), а S₀  может быть определена при вычислениях, показанных в третьем методе расчета глубины ловушек;T_m – температура в градусах Кельвина.

В методе Лущика используется спадающая высокотемпературная часть пика ТСЛ:

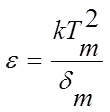      при m=1, 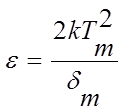                при m=2,                    (2.15)

где d_m – полуширина пика со стороны высоких температур,  рис.7.

Для метода расчета глубины ловушки по полному пику ТСЛ прологарифмируем уравнение (2.13):

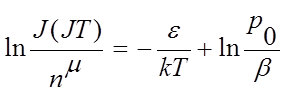                                    (2.16)

Полученное уравнение (2.16) есть уравнение прямой в координатах, представленных на рис.8. Учитывая, что концентрация центров захвата при заданной температуре n ~ S(T), получаем, что глубина ловушки e может быть определена как тангенс угла наклона прямой 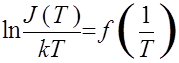, (рис.8). Причем величина S(T) определяется как площадь под экспериментальной кривой J(T). Для расчета глубины ловушки e можно использовать J и S в относительных единицах, т.к. численный множитель под знаком логарифма не будет влиять на наклон прямой, соответствующей уравнению (2.16).

Если процесс имеет первый порядок кинетики (m=1), то может быть также определен и  частотный фактор р₀:

          (метод Урбаха)