Термостимулированная люминесценция твердых тел: Учебное пособие, страница 4

Аналитическое выражение для кривой термовысвечивания можно получить, лишь сделав ряд упрощающих предположений. По-прежнему будем считать, что имеется лишь один вид электронных ловушек с одной и той же глубиной залегания e. Примем, далее, что каждый освобожденный из ловушки электрон обязательно рекомбинирует с положительной дыркой с испусканием люминесценции. Это равносильно предположению, что в уравнении (1.4) b/g = 0. В этом случае из уравнений (1.4) и (1.5) получаем

I = dn/dt= -rn.                                                                                  (2.1)

Перевод электронов из ловушки в зону проводимости происходит в результате термического возбуждения, при котором электроны приобретают энергию, достаточную для преодоления энергетического барьера ε. Электроны в ловушках имеют максвелловское распределение по энергиям, и вероятность ρ освободиться электрону в единицу времени из ловушки глубиной ε при температуре Т  имеет вид

,    (2.2)

где ν — коэффициент, имеющий размерность частоты и связанный с частотой колебаний кристаллической решетки, иногда называется частотный фактор; k — постоянная Больцмана.

При термовозбуждении можно задать любую программу нагрева люминофора. Примем, что нагрев кристалла происходит с постоянной скоростью, так что

                 Т = Т₀ + βt  ,                                                                                     (2.3)

где Т₀ — температура в начальный момент времени; t — время нагрева, β -постоянный коэффициент. Подставив выражение (2.2) в формулу (2.1), получим

(2.4)

или

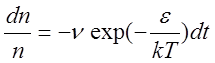.                                                                           (2.5)

Из формулы (2.3) получаем

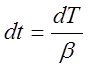
и после интегрирования

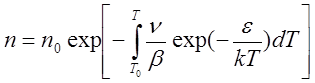 .                                                                    (2.6)

Из формул (2.1), (2.4) и (2.6) получим следующее выражение для интенсивности люминесценции:

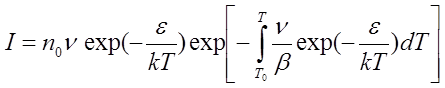.                                               (2.7)

Формула (2.7) является математическим представлением кривой высвечивания для фосфоров, имеющих ловушки только одного типа. Значение интенсивности по этой формуле можно определить лишь приближенно путем численного интегрирования.

На рис. 5 показана зависимость интенсивности Iот температуры Т, рассчитанная по формуле (2.7) для различных значений ε и ν.

Рис.5. Теоретическая зависимость интенсивности люминесценции I от температуры T при различных значениях параметров ε и ν: ε₁<ε₂<ε₃<ε₄; ν₁>ν₂>ν_3.

Вначале с повышением температуры интенсивность люминесценции увеличивается, так как растет число электронов, освобожденных из ловушек, достигает максимума при некотором значении температуры Т_m, а затем падает вследствие уменьшения запаса электронов в ловушках. Максимум сдвигается в сторону больших температур при увеличении значений ε и  β  и при уменьшении значения ν.

Из предыдущих формул легко получить

Idt = dnили        IdT = βdn.

Отсюда площадь под кривой термовысвечивания Sравна

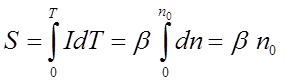.                                                         (2.8)

Здесь принято, что в результате нагрева все ловушки «опустошаются». Площадь под кривой термовысвечивания оказывается пропорциональной числу первоначально захваченных в ловушки электронов n₀; число электронов n₀, в свою очередь, пропорционально поглощенной дозе.

Для определенного типа ловушек (ε и ν фиксированы) и при заданном значении скорости нагрева β высота пика также пропорциональна числу электронов n₀, а следовательно, и дозе. Таким образом, есть две возможности определения дозы излучения: по измерению площади под кривой высвечивания (интегральный метод) и по высоте пика при температуре Т_m(пиковый метод).

Если кристалл содержит несколько различных типов ловушек, то каждая из них характеризуется своими значениями ε и ν;   кривая высвечивания в этом случае имеет несколько пиков. Те ловушки, которые имеют низкое значение ε и большое ν, плохо сохраняют запас энергии. Так, ловушки с глубиной залегания ε≤0,8 эВ и со значением ν≥10⁹ с^-1 заметно опустошаются в течение нескольких часов при комнатной температуре.