Принцип Гюйгенса-Френеля в несколько упрощенном виде можно сформулировать так: если существует источник монохроматического излучения с распределением на некоторой поверхности комплексной амплитуды поля U1(x1,y1,z1), то поле U2(x2,y2,z2) в любой точке пространства с координатами (x2,y2,z2) является суперпозицией сферических волн от каждой точки (x1,y1,z1)поверхности источника. Другими словами, электромагнитное поле в любой точке пространства есть результат интерференции сферических волн от каждой точки поверхности источника. Под источником подразумевается любая, даже воображаемая поверхность в пространстве, например, плоскость, на которой известно распределение комплексной амплитуды поля.
Математической формулировкой принципа Гюйгенса-Френеля является диффракционное уравнение Френеля-Кирхгофа:
U2(x2,y2)=-iR/4π ∫∫exp(iRr12)/r12*[1+cos(ň,ř12)]U(x1,y1)dx1dy1 (2)
где: x1,y1 и x2,y2 - поперечные координаты точек на плоскости источника и параллельной ей плоскости наблюдения, ř12- радиус-вектор, соединяющий эти точки, ň - нормаль к плоскостям источника и наблюдения, R = 2π/λ, - волновое число, λ - длина волны излучения. Здесь среда считается однородной, источник - строго монохроматическим, так что комплексная амплитуда поля U(x,y,t)=U(х,у)ехр(-iωt) и действительная величина напряженности поля равна Re[U(х,у) ехр(-iωt)]. Интенсивность излучения для монохроматического источника I(х,у) = U(х,у)2.
В теории оптических резонаторов, как правило, имеем дело с так называемыми параксиальными пучками, углы наклона которых к оси системы малы, это позволяет положить cos(ň,ř12) I. В большинстве случаев расстояние L между плоскостями источника и наблюдения велики по сравнению с поперечными размерами области, где поле имеет ненулевую интенсивность. Это позволяет в показателе экспоненты заменить на приближенное ř12L + (х2-х1)2/2L + (у2-у1)2/2L, а в знаменателе вместо ř12 подставить просто L. Так получаем формулу, которую обычно называют приближением Френеля:
U2(x2,y2)= exp(iRL)/iλL∫∫U(x1,y1)exp[[(х2-х1)2 +(у2-у1)2]iR/2L]dx1dy1 (3)
1.3. Распространение излучения через оптическую систему.
В случае распространения излучения через некоторую оптическую систему преобразование комплексной амплитуды поля сохраняется подобным по форме выражению (3), приобретая лишь дополнительные коэффициенты [2]:
U2(x2,y2)=exp(iRL)/iλB∫∫U(x1,y1)exp[[A(х22-х12)+D(y22-y12)-2(x1x2+y1y2)]iπ/λB]dx1dy1 (4 )
Как видим, ур.(4) отличается от (3) только появлением коэффициентов А, В, D, представляющих собой элементы лучевой матрицы, описывающей оптическую систему.
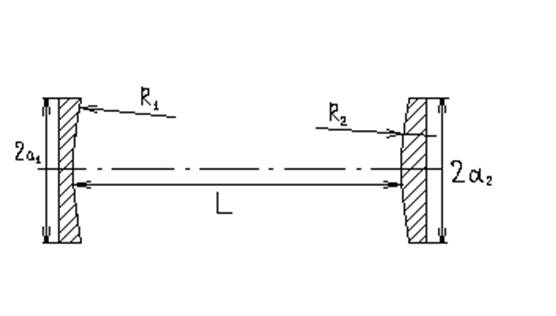
Если оптическая система - это резонатор лазера (рис.1), состоящий из 2-х зеркал с радиусами кривизны R1 и R2, установленных на расстоянии l, то лучевая матрица, соответствующая полупроходу излучения от зеркала 1 к зеркалу 2, имеет следующие элементы [2]:
A=1-L/R1; B=L;
C=-1/R1-1/R2-L/R1R2; D=1-L/R2; (5)
На практике в большинстве лазеров зеркала и, соответственно, лазерные пучки имеют круглую форму, и для них удобно ввести цилиндрические координаты, тогда (4) преобразуется к виду:
a1 2π
U(r2,φ2)= exp(iRL)/iλB∫ ∫U(r1,φ1)exp[(Ar12+Dr22)iπ/λB]*
0 0
*exp[-r1r2cos(φ1-φ2)]iR/B]r1dr1dφ1 (6)
здесь и далее а1 и а2 обозначают радиусы апертур зеркал.
Рис.1.
Полагая кроме того, что изменение поля по азимуту описывается синусоидальной функцией Ul(rn,φn)= Ul(rn)ехр(-ilφn), где l=0,1,2..., можно выполнить интегрирование по углам. После интегрирования получаем, учитывая интегральное представление функций Бесселя (см., например, [3]):
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.