Информатика и выч. техника \ Моделирование систем и комплексов

Моделирование непрерывных случайных величин, заданных графиком: Отчёт по компьютерному практикуму "Генераторы непрерывных случайных величин"

Страницы работы

16 страниц (Word-файл)

Скачать файл

Содержание работы

Министерство общего и профессионального образования

Российской Федерации

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ, МЕХАНИКИ И ОПТИКИ

ОТЧЁТ

ПО КОМПЬЮТЕРНОМУ ПРАКТИКУМУ

Генераторы непрерывных случайных величин

по теме:

МОДЕЛИРОВАНИЕ СЛУЧАЙНЫХ ВЕЛИЧИН

(промежуточный)

Исполнитель темы,

студент группы 3513 _____________ Воробей И.А.

^{подпись, дата}

Преподаватель _____________ Д.Г. Николаев

^{подпись, дата}

Санкт-Петербург 2008

РЕФЕРАТ

В отчете 14 с., 7 рис., 1 прил.

ОТЧЕТ ПО КОМПЬЮТЕРНОМУ ПРАКТИКУМУ «ГЕНЕРАТОРЫ НЕПРЕРЫВНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН»

Объектом исследования работы является моделирование непрерывных случайных величин, заданных графиком.

Цель работы заключается в ознакомлении с моделью генератора и влиянием параметров на добротность генерации непрерывных случайных величин, построении модели генератора, оценке и анализе его характеристик.

Задание на компьютерный практикум:

Смоделировать непрерывную случайную величину, заданную графиком (рис 1):

Рис 1

Оценить математическое ожидание полученной непрерывной случайной величины.
Оценить дисперсию полученной непрерывной случайной величины.
Построить доверительный интервал, соответствующий доверительной вероятности β = 0.95.
Оценить корреляционную функцию для полученной дискретной случайной величины по графикам ( j, p( j)) и ( X_j, X_j_{+ 1}) (при построении графика ограничиться первыми 20 значениями).
Проверить гипотезу о законе распределения (методом гистограмм)

Результатом работы является получение программы экспериментальных исследований, содержащей в себе решение поставленных задач.

ВВЕДЕНИЕ

Одной из важных областей генерации случайных чисел является генерация псевдослучайных непрерывных величин.

ОСНОВНАЯ ЧАСТЬ

1. Суть метода генерации непрерывных случайных величин основывается на модели линейного конгруэнтного генератора равновероятной последовательности, в основе которого лежит зависимость следующего элемента последовательности от предыдущего, описываемая формулой:

x_i+1= (а*x_i + с) mod m, (1)

где a, c, m - целые положительные константы.

Допустим, нам требуется смоделировать непрерывную случайную величину, заданную графиком (рис. 2):

Рис 2

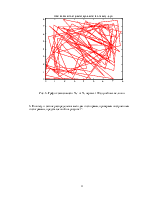
Для этого мы сгенерируем две последовательности равной вероятности с помощью линейного конгруэнтного генератора: последовательность X в интервале от X₁ до X₂, и последовательность Y в интервале от 0 до Y. После чего, рассматривая i-тые элементы этих двух последовательностей как координаты i-той точки на декартовой плоскости, отберём абсциссы только тех из них, которые попадают в закрашенную область на рис. 2, т.е. удовлетворяют условию генерации. Таким образом, полученный массив абсцисс и будет множеством сгенерированных значений непрерывной случайной величины.

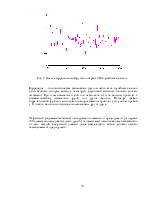
В данном практикуме требуется сгенерировать последовательность непрерывных величин, заданных графиком распределения (рис. 3):

Рис. 3

В качестве значений параметров генератора Леммера выберем значения: a = 17, c=3, m=1024, X₀=10, Y₀=500. Таким образом, генерация непрерывных последовательностей X, Y производиться по формулам:

x_i+1= (17x_i + 1) mod 512, (2)

y_i₊₁= (17y_i + 1) mod 512, (3)

После чего производится деление всех элементов непрерывных последовательности на коэффициент m и домножение на коэффициенты 4 и 0.5 соответственно, чтобы полученные последовательности находились в интервалах: X: (0,4), Y: (0, 0.5). Затем выбирая из пар (x,y) абсциссы тех точек, которые удовлетворяют закрашенным на рис. 3 областям, получаем последовательность непрерывной величины.

Сгенерируем последовательность в системе MatLab 7.0:

%определение параметров

a=17;

c=3;

m=1024;

x(1)=10;

y(1)=500;

num=2000;

%генерация и вывод последовательности

disp('Последовательность случайных чисел по методу Лемера: ');

for i=2:num

x(i)=mod(a*x(i-1)+c,m);

y(i)=mod(a*y(i-1)+c,m);

end;

for i=1:num

x(i)=x(i)/m*8;

y(i)=y(i)/m*0.25;

end;

N=0;

sum=0;

xx=0;

for i=1:num

if x(i)<=2

if x(i)>4*y(i)

N=N+1;

xx(N)=x(i);

disp(xx(N));

sum=sum+xx(N);

end;

elseif x(i)>=2.01&x(i)<=3.99

if x(i)>4*y(i)+2;

N=N+1;

xx(N)=x(i);

disp(xx(N));

sum=sum+xx(N);

end;

elseif x(i)>=4&x(i)<=5.99

if x(i)>4*y(i)+4;

N=N+1;

xx(N)=x(i);

disp(xx(N));

sum=sum+xx(N);

end;

elseif x(i)>=6&x(i)<=8

if x(i)>4*y(i)+6;

N=N+1;

xx(N)=x(i);

disp(xx(N));

sum=sum+xx(N);

end;

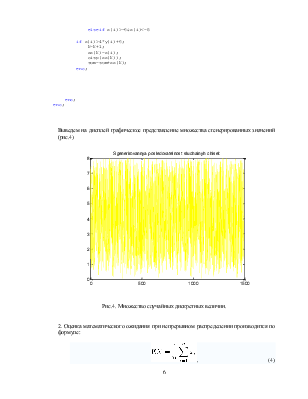
Выведем на дисплей графическое представление множества сгенерированных значений (рис.4)

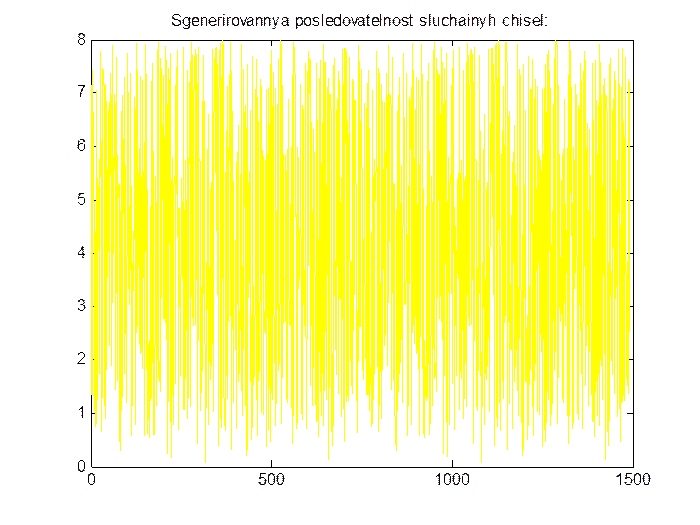
Рис.4. Множество случайных дискретных величин.

2. Оценка математического ожидания при непрерывном распределении производится по формуле:

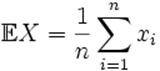$\mathbb{E}X = \frac{1}{n} \sum\limits_{i=1}^n x_i$ , (4)

где x_i- i – ый элемент последовательности, n – количество чисел в последовательности.

Сформулируем данную задачу в MatLab:

mu=0;

disp('Оценка мат. ожидания: ');

for i=1:7

mu=mu+xi(i)*pi(i);

end;

disp(mu);

При данных значениях параметров среда возвращает значение математического ожидания, равное 4.2164

3. Оценка дисперсии полученной последовательности производится по следующей формуле:

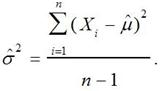(5)

Сформулируем это на языке MatLab 7.0:

disp('Оценка дисперсии: ');

sum2=0;

for i=1:N

sum2=sum2+(x(i)-mu)^2;

end;

d=sum2/N;

disp(d);

В нашем случае дисперсия равна 4.2809.

4. Оценка некоторого неизвестного параметра a одним числом называется точечной оценкой. В ряде случаев для параметра a необходимо не только найти численное значение, но и оценить его надежность и точность. Требуется знать - к каким ошибкам может привести замена параметра a его точечной оценкой, и с какой уверенностью можно ожидать, что ошибки не выйдут за известные пределы. Чтобы дать представление о точности и надежности оценки a, в математической статистике вводятся понятия доверительного интервала и доверительной вероятности.

Пусть из ряда экспериментов для параметра а получена несмещенная оценка , т.е. оценка, для которой выполняется условие