Область применимости классической механики. Межатомные силы (потенциалы)

Лекция 4

4. Область применимости классической механики. Межатомные силы (потенциалы)

Нам необходимо рассмотреть потери энергии движущейся частицы, обусловленные упругими соударениями с ядрами (атомами) мишени. Подобным образом быстрый бильярдный шар теряет энергию при столкновении с покоящимися или медленно движущимися шарами. Это один из основных «каналов» потерь энергии для тяжелых заряженных частиц (ускоренных ионов, осколков деления). Это же относится к образующимся и движущимся в среде атомам (ионам) отдачи, а также к нейтральным нейтронам.

Для того, чтобы сосчитать эти потери, надо вычислить долю атомов отдачи в интервале от Е₂ до E₂ +dE₂ (образуемых тормозящейся движущейся частицей с текущей энергией E) т.е. знать функцию f(E₂) распределения атомов отдачи по энергиям. Это необходимо, чтобы подсчитать <E₂(E))>, для чего, в свою очередь, надо знать функцию углового распределения атомов отдачи g(φ).

Функцию же углового распределения атомов отдачи можно определить (как это будет показано в лекции 5 при общетеоретическом рассмотрении задачи о столкновении), лишь детально зная силы взаимодействия частиц М₁ и М₂, т.е. имея в распоряжении потенциал взаимодействия этих частиц.

Мы говорили, что мы можем ограничиться в расчетах нерелятивистским подходом, пользуясь уравнениями классической механики, т.к. при Е₁ < 10– 10⁷ эВ для тяжелых заряженных частиц справедливо соотношение:  u₁ << c (это же относится и к U₁, V₁ при переходе к с-системе).

В этой лекции мы займемся анализом потенциалов, но, перед этим, надо решить вопрос о том, когда задача взаимодействия частиц требует квантово-механического рассмотрения, а когда она может быть решена в классическом приближении.

4.1. О границах применимости классического приближения

Классическое приближение справедливо, если:

1. Неопределенность координаты гораздо меньше характерного размера области (а) сильного взаимодействия

                                                    (4.1)

(величина а – порядка радиуса частиц мишени: a~R).

2. Неоднозначность угла отклонения падающей частицы также должна быть достаточно мала. С учетом того, что сильная дифракция имеет место для малых углов порядка , второе условие гласит

A’ O  A

   

R

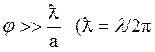)                                                              (4.2)

Действительно, сильная дифракция имеет место, когда источник виден под углом, вмещающим малое число зон Френеля. Если угол вмещает две зоны Френеля (Рис. 4.1), то

             

MA=h+λ/2, R²=(h+ λ/2)²-h²≈λh

M                                 h=R²/λ,  φ = tg φ ≈ R/h,   φ ~ λ/R, т.е. φ ~ λ/a    (a=A’A/2).

Рис. 4.1

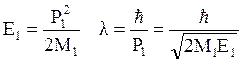                                              (4.3)

            Это можно записать в более удобной форме, если ввести радиус Бора (а₀) и постоянную Ридберга (E_R). Для водородоподобных атомов (ионов), используя исходное предположению Бора о квантовании момента количества движения электрона:

      (n=1,2, … ),                                                                (4.4)

а также закон Кулона и 2-й закон Ньютона: 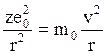   (где m₀ и a₀ – масса и заряд электрона, v²/r – центростремительное ускорение), для энергий электронных уровней и a₀ получаем:

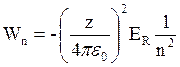  (СИ)    и                                           (4.5)

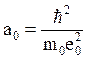,     (при n = 1, r₍₁₎ = a₀ - радиус Бора)   (4.6)

где 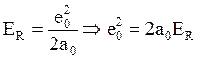                                                 (4.7)

(a₀ = 0,53 Ǻ,  E_R = 13,6 эВ - постоянная Ридберга).

Тогда, с учетом (4.6) и (4.7),

.(4.8)

           

В итоге  условие 1                                        ,           ,                ,                                         (4.8)

запишется в виде:    

Е₁ >> Е* 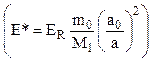     ,                                       (4.9)

а  условие 2 -  виде:                                     φ²E₁ >> E*.                                                    (4.10)

Поскольку φ ≤ 1,  второе условие является более жестким.

Таблица 4.1

Величины  E^* и ₁