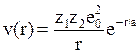Область применимости классической механики. Межатомные силы (потенциалы), страница 3

,                                          (4.14)

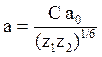            .                                                  (4.15)

где а – это эффективная область взаимодействия (радиус мишени), С – безразмерная постоянная порядка единицы. Очевидно, что этот потенциал переходит в простой кулоновский при r → 0 (r << a). Бор дал другое выражение для знаменателя: , но характер зависимости остается аналогичным.

В потенциале Томаса-Ферми два важных члена: при r << a₀ - простой кулоновский потенциал, а при r ~ a₀ существенную роль играет множитель, учитывающий экранировку.

5. В области а₀ < r < D главный вклад дают электронные взаимодействия, потенциал Т-Ф этого не учитывает. Это учел Абрахамсон, используя статистику Ферми-Дирака. Он получил потенциал, который называют потенциалом Абрахамсона или Томаса-Ферми-Дирака. Этот потенциал не имеет простого аналитического выражения.

Глубина взаимного проникновения электронных оболочек уже при Е₁ = 1–10 кэВ достаточно велика.

Абрахамсон рассчитал V(r) для всех видов комбинаций инертных газов и получил, что при r > a₀ c достаточно хорошей степенью точности пригоден потенциал Б-М: V(R) = A e^–r/b, где b = a₀/2 и A(z) ~ A z^3/2.

Для пар N-Ne, Nc-F^–, Ar-Ar, k⁺Cl^–, Cu-Cu, Kr-Kr, Pb⁺-Br^–, Xe-Xe, Cs⁺-I^–, Au-Au значения z₁ z₂, A (эВ) и b (Å) рассчитаны и приведены в таблицах (см., например, монографию Томпсона). Таким образом, можно обоснованно применять потенциал Борна-Майера для щелочных металлов или для щелочно-галоидных кристаллов, где электронные конфигурации подобны атомам инертных газов. Это же относится к благородным металлам.

Для переходных металлов при r < a₀ ошибка несущественна, но электронный член должен отличаться, поэтому A и b находят из эксперимента.

4.3. Сопоставление теории и эксперимента

При r < a₀ данные получают из наблюдения рассеяния ионов на атомах, а именно, по величине пробегов. Классические опыты Резерфорда показали, что при r << a₀ (рассеяние α-частиц достаточно высоких энергий: 10–100 МэВ) справедлив простой кулоновский потенциал.

Для несколько больших значений r Эверхарт и Лейн установили, что пригоден экранированный кулоновский потенциал Томаса-Ферми при С ≈ 0,7.

Для тяжелых ионов с энергией Е ~ 10⁵ кэВ важно значение V(r) вблизи r = a₀. Значение С получается равным 1–2. Это говорит о том, что при r = a₀ один экранированный потенциал слишком мал, и надо добавлять член типа Б-М.

При a₀ < r < D результаты хорошо описываются потенциалом Б-М:  V(r) = A e^–r/b.

Для металлов мало данных по проникновению ионов. Бринкман показал для Ag, Cu и Au, что согласие с потенциалом Б-М достигается, когда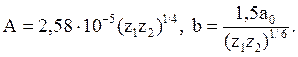

4.3. Приближенное представление потенциалов

Имеются достаточные основания, чтобы представить полный потенциал для взаимодействующих частиц (ускоренных частиц и частиц мишени) в виде экранированного кулоновского потенциала (потенциала Томаса-Ферми) и потенциала Борна-Майера*:

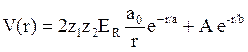.                                (4.16)

Коэффициенты A и b, подбираются соответственным образом. На малых расстояниях преобладает первый член, на больших – второй ().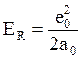

Бринкмэн предложил потенциал с аналогичными свойствами

,                              (4.17)

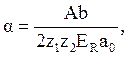                                                (4.17а)

Переходящий, при малых r, в потенциал Т-Ф, а при больших – в потенциал Б-М.

Можно представить V(r) как const/r^l. При этом в каждом ограниченном диапазоне значений r можно подобрать const и значение l. Такой вид V(r) достаточно часто используют, т.к. он позволяет получить аналитические решения для величины потерь энергии.

В частности,  для значений r, близких к a, используют обратноквадратичную функцию (l = 2):

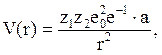                                       (4.18)

которая получатся из потенциала Томаса-Ферми :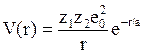 домножением на  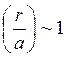(с учетом, что e^-r/a ≈ e^-1; ).

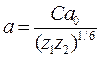При С ≈ 1 получаем

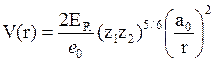,                                       (4.19)

Поскольку 2E_R/e ≈ 10 (2R=27.2 эВ, e≈2.72), то можно записать удобный для численных расчетов потенциал

	Эв

 

(4.20)