Область применимости классической механики. Межатомные силы (потенциалы), страница 2

Частица	Атом мишени		Е* << φ2Е1, эВ	, эВ
Электрон	Li	1,4*	–	104
– " –	U	1,5	–	106
Протон	Li	1,8	10–2	10
– " –	U	4,6	10–3	103
Тяжелый ион (М1 = 100)	Li	3,8	10–4	10
– " –	U	5,7	10–6	103
*Примечание.   Далее будет показано, что (a0/a)2 ~ (z1z2)1/3.

Для заряженных частиц с массой, по крайней мере, не меньшей массы протона, классическое приближение справедливо. Хотя электрон заряжен и имеет величину а, сравнимую с величиной а для протона, его масса очень мала, и его столкновения должны быть отнесены к разряду квантовых.

Кроме того, энергия электрона должна иметь порядок m₀с² (~0,5 МэВ), чтобы представлять интерес для теории атомных повреждений (Е₁ ≥ m₀с²), поэтому необходимо применять релятивистскую квантовую механику. Уравнение  при этом не выполняется. Для электрона

 

,                                (4.11)

см. лекцию 9.

4.2. Межатомные силы. Способы описания

Это наиболее фундаментальный вопрос, без анализа которого невозможно детально рассматривать задачу о столкновении частиц.

Межатомный потенциал V(r) учитывает взаимодействие между электронами и ядрами сталкивающихся частиц. Мы уже ввели боровский радиус. Обозначим через D расстояние между ближайшими атомами в кристалле (за характерную величину D для большинства кристаллов можно принять:  D ~ 2,5 Å). Проведем качественную графическую (достаточно грубую) классификацию используемых потенциалов.

            Атом водорода

 

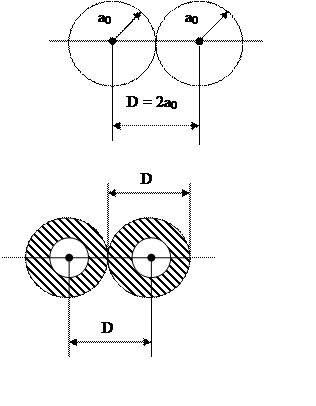Атомы вещества мишени

(графики даны в планетарной модели)                                          

1.  r≥D , электронные оболочки не перекрываются (r – расстояие между частицами). Справедлив потенциал Борна-Майера (Б-М, см. ниже)

 

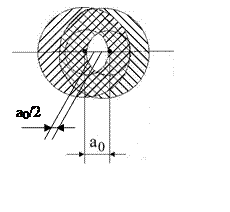2.  Между ядрами уже нет электронов. Если r<a₀/2, справедлив простой кулоновский потенциал.

3.  a_o/2≤r<D, справедлив экранированный кулоновский потенциал Томаса-Ферми (Т-Ф) и другие правдоподобные потенциалы (см. ниже).

1. При сближении атомов их внешние оболочки перекрываются, образуются химические связи (ионная, ковалентная, металлическая). Существуют также  ван-дер-ваальсовы силы (межмолекулярные). Соответствующие энергии очень малы (порядка нескольких эВ), и при энергиях бомбардирующих частиц, достаточных для создания радиационных повреждений (т.е. имеющих на порядки большие энергии), этими взаимодействиями можно пренебречь.

2. Когда a₀ < r < D, перекрываются внутренние заполненные оболочки. По принципу Паули это ведет к повышению энергии (электроны могут только подниматься по энергии, т.к. только два электрона могут находиться в одном состоянии). Этот эффект известен как эффект отталкивания заполненных атомных оболочек и дает важный вклад в потенциальную энергию в этой области.

Разными авторами было найдено, что для пар инертных газов при а₀ < r < D справедлив следующий вид потенциала:

V (r) = A e^–r/b.                                (4.12)

Он был использован для ионных кристаллов Борном и Майером и получил название потенциала Борна-Майера. В ионных кристаллах ионы имеют такую же конфигурацию, как инертные газы и для них этот потенциал также справедлив.

3.  Когда r << a, и ядра становятся ближайшей парой наиболее сильно заряженных частиц в системе, их потенциал преобладает над потенциалом других заряженных частиц (электронов). В этом случае справедлив простой кулоновский потенциал

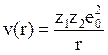.                                                (4.13)

4. При увеличении r в пространстве между ядрами оказываются сначала самые глубокие внутренние оболочки. Теперь мы имеем дело уже с экранированным кулоновским потенциалом. Томас и Ферми предложили метод расчета эффективной плотности заряда вокруг атома и оценили V(r). Простой функции нет, но при r > a₀ хорошим приближением является функция