Взаимодействие быстрых электронов с веществом

Лекция 14

14.1. Взаимодействие быстрых электронов с веществом.

Для электронов относительно малых энергий потери энергии в веществе, обусловлены ионизацией и возбуждением связанных электронов. Этот механизм мы рассматривали в случае торможения тяжелых заряженных частиц. При высоких же энергиях потери обусловлены в основном испусканием электромагнитного излучения в тормозящем поле.

Согласно классической электромагнитной теории электрический заряд, испытывающий ускорение излучает энергию мощностью

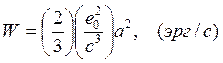                            (14.1)

где е₀ – заряд электрона, c – скорость света в вакууме, а – ускорение.

В электрическом поле ядра электрон будет испытывать ускорение а ~ Z/m (m – масса электрона) гораздо большее, чем тяжёлые частицы. Потери энергии на излучение, согласно (14.1), будут в этом случае на несколько порядков выше, чем при торможении тяжелых заряженных частиц (Z – заряд ядер мишени, т.к. торможение происходит в поле ядра). Излучая электромагнитную энергию электрон тормозится, поэтому такое излучение называется тормозным.

Излучение протона в ~ 3·10⁶ раза меньше ускорения электрона и для него тормозное излучение практически не даёт вклада в потери энергии. Для тяжёлых же ионов потери в 10⁹ - 10¹⁰ раз меньше.

Таким образом, при торможении быстрых электронов нужно учитывать как ионизационные потери, так и радиационные (на тормозное излучение). Чтобы увеличить тормозное излучение надо увеличивать Z. Для получения мощных потоков излучения обычно используется вольфрам (Z=74). Вольфрам к тому же является термостойким.

14.1.1.Ионизационные потери для электронов.

Теория была разработана Бете, как часть общей теории торможения заряженных частиц. Бете были выполнены квантово-механические расчёты в 1930 г.

Для тяжёлых заряженных частиц при нерелятивистских скоростях но больших скоростей электрона в атоме (E > 10⁸ эВ)

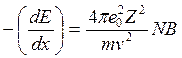,                                (14.3)

где Z и v – заряд и скорость частиц (v > v₀, где v₀ – скорость электрона на первой боровской орбите атома водорода), m – масса частицы, B – коэффициент торможения вещества, N – число атомов в 1 см³.

При нерелятивистских скоростях

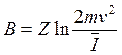,                                (14.4)

где - средняя энергия возбуждённого атома среды ( находится из экспериментальных данных). Для воздуха, на пример, = 80,5 эВ, для алюминия 150 эВ. Для лёгких элементов (Z < 15) » 11,5·Z эВ, а для более тяжёлых  » 9·Z эВ.

Для тяжелых заряженных частиц в случае релятивистских скоростей

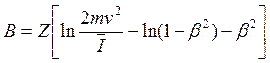,                            (14.5)

Для нерелятивистских электронов

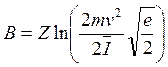,                                  (14.6)

где e – основание натурального логарифма.

Для релятивистских скоростей электронов

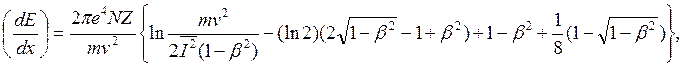(14.7)

где .

Значение  для нерелятивистских протонов и электронов отличаются лишь малым множителем, стоящим под знаком логарифма, поэтому протоны и электроны с одинаковой нерелятивистской скоростью будут терять энергию примерно одинаково.

Электроны выбитые из атомов в процессе ионизации называются  – электронами. Эти  – электроны также могут вызывать ионизацию. По пробегу  – электронов, их числу и углу вылета можно оценивать энергию ионизирующих частиц. Это очень важно для расчётов защиты.

Вследствие малой массы электронов число актов рассеяния, определяющих заданную потерю энергии ΔE для электронов значительно больше, чем для тяжёлых заряженных частиц. Многократное рассеяние значительно увеличивает путь электронов в веществе  заданной толщины. Это сильно усложняет измерение потерь  электронов в конденсированных средах. Трудности настолько велики, что при снижении энергии мы подходим к некому пределу, когда рассчитать потери практически невозможно.

Быстрые электроны движутся прямолинейно, лишь незначительно отклоняясь за счёт рассеяния. По мере того, как энергия уменьшается, роль рассеяния возрастает и имеет место гауссовское распределение рассеянных электронов по углу. При увеличении толщины образца, гауссовское распределение становится настолько диффузным, что не существует какого – либо преимущественного направления и перемещение электронов можно рассматривать как диффузию. Угловое распределение перестаёт изменяться с увеличением толщины фольги.

Толщина фольги, при которой практически не один электрон не проходит через неё характеризует эффективный пробег электронов.

Эффективный пробег значительно меньше истинного пробега с учетом многократных столкновений. Теоретический расчёт эффективного пробега электронов в конденсированных средах практически невозможен (хотя возможно моделирование методом Монте-Карло).

Экспериментально пробег находят методом наложения тонких фольг из исследуемого материала.

Для характеристики поглощения электронов часто пользуются так называемым “слоем половинного поглощения” Δх (слой ослабляющий поток электронов в двое).

Установлено, что для немоноэнергетических пучков электронов ослабление потока происходит по закону, близкому к экспоненте.

,                                          (14.8)

где μ – линейный коэффициент ослабления потока β частиц (если x измеряется в [г/см²], то используют μ_m = μ/ρ – массовый коэффициент поглощения [см²/г]).

14.1.2. Потери энергии на излучение для быстрых электронов (радиационные потери).

Полное рассмотрение было проведено рядом авторов, в том числе, Бете и Гайтлером в 1934 г. Использовали уравнение Дирака для электрона и борновское приближение для описания взаимодействия электрона с ядром. Потери существенно зависят от экранирования ядра электронами. Для различных условий экранирования получается различный результат, но во всех случаях радиационные потери увеличиваются с ростом Z, N и E:

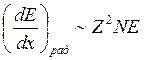,                                        (14.9)

Ионизационные же потери

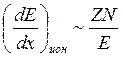.                                             (14.10)

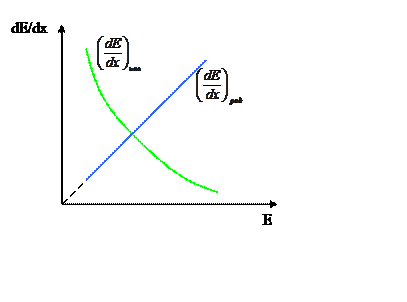
Поэтому при относительно низких энергиях преобладают ионизационные потери, а при высоких – радиационные (на электромагнитное излучение).

Есть приближенное соотношение Бете – Гайтлера, в близи критической энергии

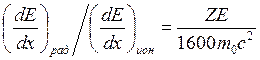                                           (14.11)

(m₀c² » 0,5 МэВ для электрона) и тогда

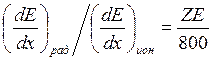.                                       (14.12)

Это позволяет найти E_кр

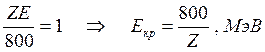.                                         (14.13)

Чем больше Z, тем при меньших энергиях существенны радиационные потери (Z – заряд ядра атомов мишени).

14.1.3. Полные потери энергии

Полные потери энергии определяются соотношением:

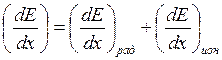.                                     (14.15)

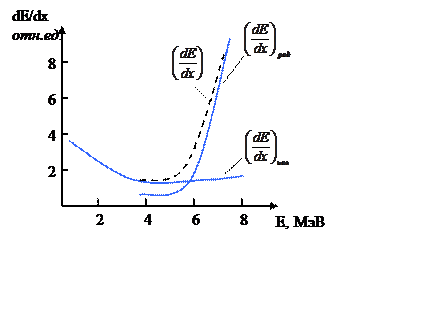
На рис. в качестве примера представлены потери энергии для свинцовой мишени.

Радиационные потери возникают не только от взаимодействий с ядрами, но и с электронами, но эти потери малы.

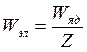,                 (14.16)

Этот результат получен Ландау и Румером в 1983 году.

То, что касается радиационных повреждений, при энергиях больше 0,5 МэВ электроны создают в материалах единичные радиационные дефекты – френелевские пары. Средний проективный пробег электронов при энергиях несколько МэВ от нескольких сотен микрон до миллиметров. Мы это рассмотрели в первых лекциях, записали сечение взаимодействия для электронов и P(E₂) пик вблизи .