Расчет асимптотических значений энергий частиц при упругом столкновении

Лекция 3

Расчет асимптотических значений энергий частиц при упругом столкновении

Если энергия отдачи (т. е. кинетическая энергия, приобретаемая атомом отдачи) больше энергии образования радиационного повреждения, происходит выбивание атома из его устойчивого положения в твердом теле.

Обозначим параметры сталкивающихся частиц в лабораторной системе координат (связанной с частицей-мишенью, т. е. в так называемой l-системе). Пусть M₁, , E₁ – масса, скорость и кинетическая энергия налетающей частицы (до столкновения), а θ₁ и – ее угол рассеяния и конечная скорость; М₂ =и Е₂=0 – масса, скорость и кинетическая энергия второй частицы, частицы-мишени (до столкновения), аи θ₂ – ее конечная скорость и угол отдачи.

Уравнения упрощаются в системе, связанной с центром масс сталкивающихся частиц (в так называемой с-системе).

 

G                 М₁,                            

M₁,          (М₁+М₂),

М₂,

В лабораторной системе импульс центра масс равен сумме импульсов частиц

.                                                                                                                                              (3.1)

или

, откуда

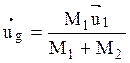                                                                                                                                              (3.2)

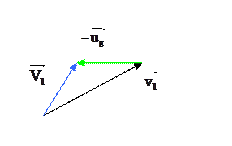
Вычитая  из всех скоростей, переходим к с-системе, связанной с центром масс.

Обозначения в с-системе:

  – скорости частиц до соударения,

  – после соударения.

Процессы в с-системе

 

М₁ до столкновения                                     М₁ после столкновения

                                      =+(–)                                                         = +(–)

            –

М₂ до столкновения                                     М₂ после столкновения

 

–

                                      =+(–)                                                      = +(–)

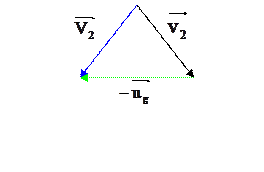
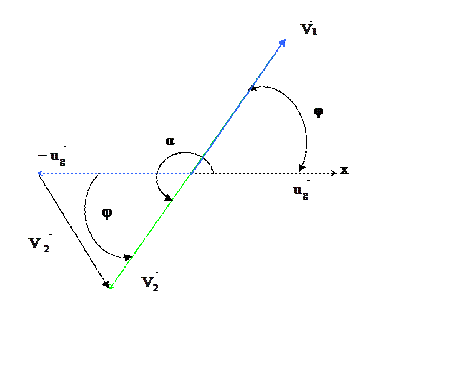
Столкновение двух тел в с-системе

Рис. 3.1.

Поскольку G остается в покое,  и  противоположно направлены.

Законы сохранения энергии и импульса имеют следующий вид:

                                                                                                                                              (3.3)

                                                                                                                                              (3.4)

Проектируя (3.4) на оси х и у, получаем

х:         M₁U₁ – M₂u_g = (M₁V₁ – M₂V₂) cos φ                        (3.5)

y:         M₁V₁ – M₂V₂ = 0       Þ        M₁V₁ = M₂V₂                        (3.6)

С учетом последнего соотношения из (3.5) следует, что

M₁U₁ = M₂u_g                                                                                                                                              (3.7)

Тогда

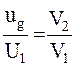.                                                                                                                                              (3.8)

Проектируем уравнение (3.4) на биссектрису угла рассеяния φ и решаем совместно с (3.3):

,                                                                                                                                              (3.9)

,                                                                                                                                            (3.10)

,

, в результате получаем:

.                                                                                                                                            (3.11)

Далее из 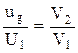                следует, что

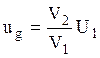, тогда

и

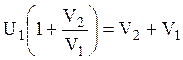, откуда следует, что

и, с учетом (3.8),

.                                                                                                                                            (3.12)

С учетом этих соотношений, проделав достаточно простые выкладки:

,

.

,                                                                                                                                            (3.14)

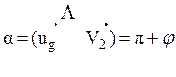                                                                                                                                            (3.15)

                                                                                                                                            (3.16)

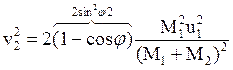
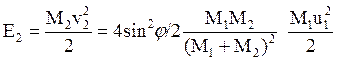
окончательно получаем:

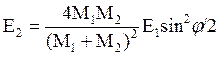                                                                                                                                            (3.18)

                                                                                                                                            (3.19)

где Е₂ – это энергия отдачи (энергия атома отдачи). Выведенное соотношение аналогично уравнению для комптоновского рассеяния γ-квантов (упругого рассеяния γ-квантов на электронах).

Величину 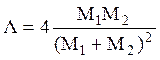 называют коэффициент передачи энергии; при φ=π  (лобовое соударение) происходит максимальная передача энергии:

                                                                                                                                            (3.20)

(в с-системе частицы при этом сближаются и удаляются по одной прямой).

Когда φ = 0, рассеяния нет, и Е₂ = 0. Для частиц, взаимодействующих на расстоянии посредством физического поля, такой случай соответствует большому значению прицельного параметра p.

 

В задачах, рассматривающих радиационные повреждения вводят минимальную  энергию , необходимую для создания радиационного повреждения.

                                                                                                                                            (3.21)

где  – минимальная энергия налетающей частицы, необходимая для создания радиационного повреждения (для которой  – максимальная энергия отдачи, которая достаточна для создания радиационного дефекта =E_d, E_d – энергия образования радиационного дефекта).

Нас будут интересовать соответственно только процессы, в которых .

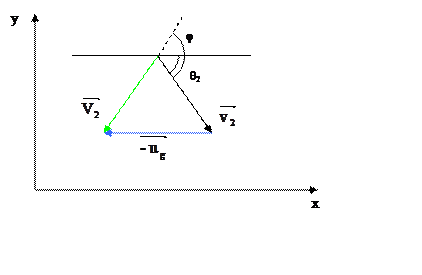
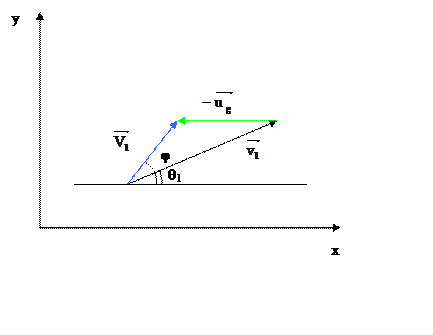
Связь между θ₂ и φ можно получить, проектируя соотношение  на оси х и у.

V₂sin φ = v₂sin θ₂                                                                                                                                                                                                                                         (3.22)

V₂cos φ + v₂cos θ₂ = u_g                                                                                                                                                                                                                                         (3.23)

Поскольку u_g = V₂, имеем

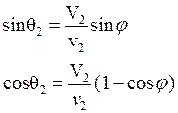
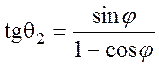                                                                                                                                            (3.24)

Аналогично, проецируя соотношение  на оси х и у, можно получить соотношение для θ₁:

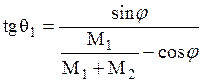.                                                                                                                                                     (3.25)