Программа статистического наблюдения совокупности коммерческих банков РФ, страница 14

Нанесем линию тренда

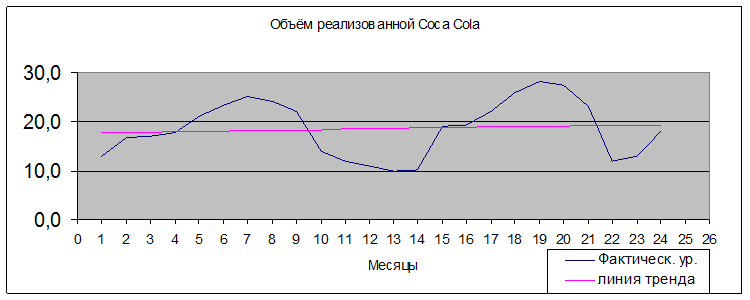
Проверим абсолютные отклонения фактических уровней на наличие автокорреляции

Найдём коэффициент автокорреляции используя критерий Дурбина-Ватсона

d= ∑(E_t-E_t-1)²/∑ Et ², предварительно сделав расчеты, занесённые в таблицу 11.3

Таблица 11.3

Год	Месяц	Абсолютные отклонения от тренда Et= уi - у*	Et-1	E_t+E_t-1	Et ²	(E_t-E_t-1)²
2002	1	-4,26	-	-	18,1476	-
	2	-0,93	-4,26	3,96	0,8649	11,0889
	3	-0,8	-0,93	0,74	0,64	0,0169
	4	-0,07	-0,8	0,06	0,0049	0,5329
	5	2,96	-0,07	-0,21	8,7616	9,1809
	6	5,39	2,96	15,95	29,0521	5,9049
	7	6,92	5,39	37,3	47,8864	2,3409
	8	5,95	6,92	41,17	35,4025	0,9409
	9	3,68	5,95	21,9	13,5424	5,1529
	10	-4,49	3,68	-16,52	20,1601	66,7489
	11	-6,46	-4,49	29,01	41,7316	3,8809
	12	-7,53	-6,46	48,64	56,7009	1,1449
2003	1	-8,77	-7,53	66,04	76,9129	1,5376
	2	-8,54	-8,77	74,9	72,9316	0,0529
	3	0,19	-8,54	-1,62	0,0361	76,2129
	4	0,52	0,19	0,1	0,2704	0,1089
	5	3,05	0,52	1,59	9,3025	6,4009
	6	6,98	3,05	21,29	48,7204	15,4449
	7	9,21	6,98	64,29	84,8241	4,9729
	8	8,24	9,21	75,89	67,8976	0,9409
	9	3,97	8,24	32,71	15,7609	18,2329
	10	-7,3	3,97	-28,98	53,29	127,0129
	11	-6,47	-7,3	47,23	41,8609	0,6889
	12	-1,44	-6,47	9,32	2,0736	25,3009
∑				544,76	746,776	383,8414

d= 383.84/746.77= 0.514

Сравниваем с d_табл. Так как d <d_табл поэтому можно утверждать о наличии автокорреляции.

Модель сезонной волны представляет собой ряд Фурье, где время выражается в радианной мере

Таблица 11.4