Программа статистического наблюдения совокупности коммерческих банков РФ, страница 10

Найдём у^,_х = а ₀+а₁х₁+а₂ х₂

nа₀ + а₁∑x₁ + а₂∑x₂ = ∑y, а₀∑x₁ + а₁∑x²₁ + а₂∑x₁х₂ = ∑ух₁.

а₀∑x₂ + а₁∑x₁х₂ + а₂∑x²₂ = ∑ух₂.

15а₀ + а₁1425,0 + а₂1647,8 = 333,5, а₀1425,0 + а₁220057,0 + а₂176260,3 =40831,4.

а₀1647,8 + а₁176260,3 + 285516,7 а₂=48612,7

а₂ =0,0986

а₁ = 0,085

а₀ = 3,325 у^,_х = 3,325+0,085х₁+0,099 х₂

Расчет показывает, что с увеличением вложений в ценные бумаги на единицу прибыль возрастает на 0,085 единицы, а с увеличением кредитных вложений на единицу прибыль  возрастает на 0,0986 единицы.

Рассчитаем частные коэффициенты эластичности Э_х=ах_ср/у_ср, где х_ср – среднее значение соответствующего факторного признака, у_ср – среднее значение результативного признака, а – коэффициент регрессии при соответствующем факторном признаке.

Э_х1= 0,085*95/22,23 = 0,36

Э_х2 = 0,0986*109,85/22,23 =0,49

Т.о. при увеличении вложений в ценные бумаги на 1% прибыль увеличивается на 0,36%, а при увеличении кредитных вложений прибыль увеличивается на 0,49%.

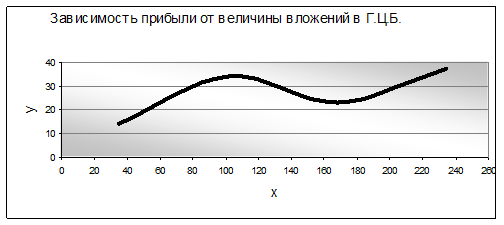
Произведем аналитическую группировку по объему вложений в ценные бумаги

вложения в ценные бумаги	середина интерв. Х1	число банков	величина прибыли у	в среднем на один банк
а	1	2	3	4
2,1-68,4	35,3	7	100,8	14,4
68,4-134,7	101,6	3	101,9	34,0
134,7-201	167,9	4	93,4	23,4
201-267,3	234,2	1	37,4	37,4

Изобразим графически:

Произведем аналитическую группировку по величине кредитных вложений

кредитные вложения х	середина интерв. Х2	число банков	величина прибыли у	в среднем на один банк
2,2-58,8	30,5	5	45,5	9,1
58,8-115,3	87,0	3	70,8	23,6
115,3-171,9	143,6	3	80,8	26,9
171,9-228,6	200,2	4	136,4	34,1

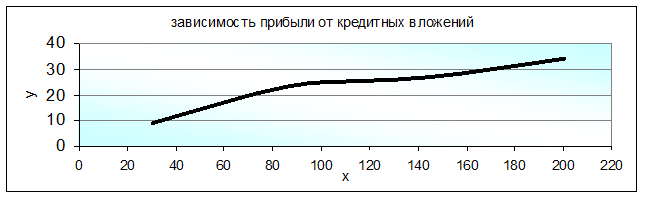Из графиков видим что между прибылью и   объемом вложений в ценные бумаги и величиной кредитных вложений наблюдается прямая зависимость.

Рассчитаем линейные коэффициенты корреляции, проверим их значимость, проанализируем характер связи.

r_yx1=  (x₁y – x ₁y)/G_x1G_y = (2556,8-35,9*22,23)/70,8*39,4=0,63, т.е. связь прямая сильная.

t_рас = √r²(n-2)/1-r = 13,9

t_табл=2,145     t_рас  >t_табл , значит коэффициент корреляции значим.

Рассчитаем r_yx2=  (x₂y – x ₂y)/G_x2G_y = (3097-30,75*22,23)/60,6*39,4= 0,889, т.е. связь очень сильная.

t_рас = 80,3 t_рас  >t_табл , значит коэффициент корреляции значителен.

Т.О.  Связь между прибылью и этими двумя показателями имеет место и значительна.

Выбранные признаки практически полностью описывают вариацию результативного признака, т.к. величина парного коэффициента корреляции R_х1х2 =(x₁х₂ – x ₁х₂)/G_x1G_х2 = 0,999 т.е. превышает 0,8.

Так как полученная модель не громоздка, следовательно,  исключать какие-либо факторы нет необходимости.

Задание10

Данные о расходах на личное потребление в США за период с 1985 по 1994 года представлены в таблице.

Таблица10.1

Расходы на личное потребление, 1985-1994г. (млрд$)