Использование кодоскопа на лекциях по методике преподавания математики, страница 2

Аналогично проводится работа с определе­ниями математических понятий на лекциях, те­мой которых является методика изучения нумера­ции (на кодопозитиве представляются основные характеристики позиционных систем счисления), математических выражений, величин, арифметиче­ских действий и т. п.

При чтении лекций по общим вопросам ме­тодики преподавания математики возникает необ­ходимость в актуализации знаний по педагоги­ке и психологии. В отдельных случаях это также можно сделать с помощью кодоскопа. Напри­мер, при чтении лекции о методах обучения математике полезно выписать на кодопозитив методы обучения в той классификации, которую преподаватель считает наиболее приемлемой для раскрытия вопросов лекции.

Эффективность использования кодопозитивов этой серии еще более повышается при одно­временном применении двух кодоскопов. Один кодоскоп используется для проецирования справоч­ных кодопозитивов, другой — для проецирова­ния кодопозитивов первой или третьей серии.

Например, на лекции по теме “Методика изучения основных величин в начальной школе” для обоснования содержания и последователь­ности рассмотрения отдельных вопросов при изучении в начальной школе конкретной величи­ны полезно в качестве справки проецировать интуитивно-содержательное описание понятия ад­дитивно-скалярной величины. Опираясь на него, преподаватель в беседе со студентами обосно­вывает содержание подготовки к ознакомлению с рассматриваемой величиной, содержание и после­довательность ознакомления учащихся со всеми вопросами, относящимися к этой величин. Постепенно это содержание, представленное в виде схемы или перечня этапов изучения данной величины, проецируется через второй кодоскоп.

При невозможности использования второго ко­доскопа роль справочного кодопозитива может выполнить таблица соответствующего содержания.

При описанной методике использования спра­вочных кодопозитивов значительно возрастает ак­тивность студентов, которые имеют возможность либо участвовать в разработке соответствующих методических рекомендаций, либо следить за ло­гикой развертывания преподавателем методиче­ских рекомендаций.

Третья серия кодопозитивов, готовящаяся к лекции, содержит образцы рекомендуемых уп­ражнений и оформления записей в тетрадях учащихся; некоторые рисунки и записи из учеб­ника по математике для I—III классов, учебных пособий;   типичные   ошибки,   допускающиеся  уча­щимися, и т. п.

Кодопозитивы третьей серии демонстрируются тогда, когда необходимо подтвердить сказанное конкретным примером.

При сообщении о том, что ознакомление уча­щихся I класса с переместительным свойст­вом сложения можно провести по рисунку, дан­ному в учебнике, на экране проецируется этот рисунок. Затем следует краткое описание содер­жания работы по данному рисунку. Все это по­могает студентам легко усваивать материал лек­ции и получать более конкретное представле­ние об оформлении учебника математики, об уп­ражнениях, имеющихся в нем, о методике ис­пользования учебника на уроке в процессе объяс­нения нового материала.

При изложении вопросов методики формиро­вания вычислительных навыков используются кодопозитивы с образцами развернутых записей и вычислений, с примерами для устного счета, с упражнениями, которые выполняются учащимися на разных этапах формирования вычислитель­ных навыков, с встречающимися типичными ошиб­ками учащихся и т. п. Упражнения берутся на­ми из тетрадей с печатной основой, пособий для учащихся или учителя, из опыта работы лучших учителей города.

Большой эффект имеет демонстрация ошибок, допущенных учащимися на уроках во время педаго­гической практики студентов. Преподаватель при этом характеризует методические недочеты студен­та в ведении урока, которые привели к этим ошиб­кам. Показ таких кодопозитивов вызывает, как правило, большой интерес у аудитории и зна­чительно повышает активность восприятия мате­риала лекции.

Разумеется, что число таких кодопозитивов, их место в лекции должно быть строги продуман­ным, показываться они должны только тогда, когда это действительно необходимо. Содержание чаще всего не переписывается полностью студентами, а лишь отражается в схематиче­ской форме или указываются источники.

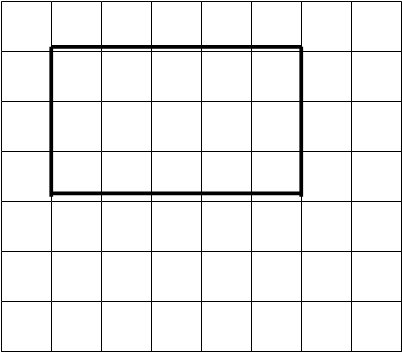
Применение кодопозитивов этой серии позво­ляет иногда сразу же на лекции показать спо­собы выполнения учащимися отдельных упражне­ний. Так, при изложении темы “Методика изу­чения площади” в лекции говорится, что фор­мированию общих представлений о площади и ее измерении способствуют упражнения в изме­рении площади фигуры с помощью моделей квадратных сантиметров или путем разбиения фи­гуры на квадратные сантиметры с помощью па­летки. Сказанное иллюстрируется показом кодопозитива с изображением фигур, представленных на рисунке 1. Преподаватель прикладывает мо­дели квадратных сантиметров к фигуре 1, за­тем прикладывает палетку к фигуре 2. Процесс измерения демонстрируется на экране.

 

                                    Рис.1.

Такая демонстрация может быть использова­на и на уроке в начальной школе, следова­тельно, студенты получают информацию и о том, как должны выполнять упражнение учащиеся, как ознакомить их с измерением площади с помо­щью модели квадратного сантиметра и как ис­пользовать для этой цели кодоскоп.

Рассматриваемая серия кодопозитивов является, таким образом, средством осуществления связи теории с практическими и лабораторными занятия­ми студентов, с практикой обучения в школе.

Кодопозитивы третьей серии полезно сочетать с показом наглядных пособий и дидактических ма­териалов для начальной школы по соответствую­щим разделам курса математики в I—III клас­сах. Однако эффективным этот прием будет тогда, когда каждая демонстрация кодопозитива и на­глядного пособия органически включается в со­держание лекции, а не образует специальный раздел ее по показу средств обучения, приме­няемых в начальной школе при изучении той или иной темы.

Умелое использование кодопозитивов при чтении лекции служит как повышению теоретического уровня, так и усилению ее практической на­правленности. Наряду с другими приемами ис­пользование кодопозитивов значительно повышает информативную емкость лекции, создает хорошие условия для усвоения материала лекции студен­тами, способствует овладению ими методикой применения кодоскопа на уроках математики в начальной школе.