Напряжения в грунте. Главные и касательные напряжения в условии плоской задачи, страница 3

При наличии полосообразной равномерно распределенной нагрузки р₀:

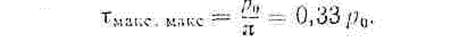
Величина касательных напряжений меняется от положения точки в пределах массива грунта основания сооружения и от ориентации площадки, проходящей через данную точку.

Пример 3. По условию примера 1 определить:

1)  величину   и   направление  максимального   касательного   напряжения в точке А;

2) величину касательных напряжений τ_xzи τ_zx в горизонтальной и вертикальной плоскостях, проходящих через точку А.

Реше н и е. Значение искомых касательных напряжений можно найти по таблицам, по графикам и аналитически.

1. По таблицам и графикам значение τ_макс определяется с учетом переходного коэффициента  ε.

Табличные значения ε для определения τ_макс даны в зависимости от угла видимости а. В условиях примера 1 угол видимости α = 22°50' .

Согласно табл. 1 приложения 2 для α = 22°50' значение переходного коэффициента ε = 0,13 (по интерполяции). По графику 1 прил. 1 при условных координатах точки А : υ= 4 И d = 2 (см.   пример 1) значение переходного коэффициента ε то же.

При   значении   равномерно   распределенной    нагрузки   р₀ = 2   кН/м²   величина   максимального   касательного   напряжения равна

τ _макс "= 0,13·2 = 0,26   кН/м².

Аналитический расчет τ_макс можно вести по формулам :

При величине главных напряжений р₁ = 0,5 кН/м² и р₂ = 0,01 кН/м² значение τ_макс  равно:

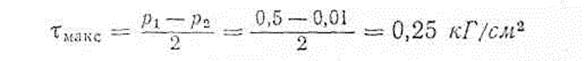
или

Максимальные касательные напряжения τ_макс  действуют по площадкам, наклоненным под углом δ = 45° к направлению действия главных напряжений (рис. 6).

 

Рис. 6. Направление действия напряжений τ_макс

Пример 4. Ленточный фундамент с шириной 2b = 2 м имеет по подошве равномерно распределенную нагрузку р₀ =1 кН/м². Построить  эпюры:

1)  максимальных  касательных напряжений τ_макс, действующих     в     точках грунтового массива на глубине 1 м;

2)  максимальных   касательных напряжений τ_макс по вертикали, проходящей по оси фундамента.

Решение.

1.       Для   построения   эпюры распределения   напряжений   τ_макс  в уровне

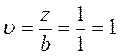 необходимо прежде всего определить углы видимости α для различных значений 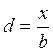 при  υ= const = 1.  По значению угла видимости (метод расчета угла видимости см. в примере 1) по табл. 1 приложения 2 определяются значения переходных коэффициентов ε и по ним значения τ_макс. Результаты расчетов сведены в табл. 1.

Построенная по этим данным эпюра распределения напряжений τ_макс показана на рис. 7.

Таблица 1

		Рис. 7. Эпюра максимальных касательных напряжений τмакс в уровне  υ = 1

 

2. Для построения эпюры распределения τ_макс по оси симметрии фундамента необходимо определить так же значения угла видимости а. Но в данном случае

увеличивается  с глубиной.

По табл.  1 прил. 2 находим значения переходных коэффициентов ε и по этим данным находим значения τ_какс (табл. 2).

Таблица 2

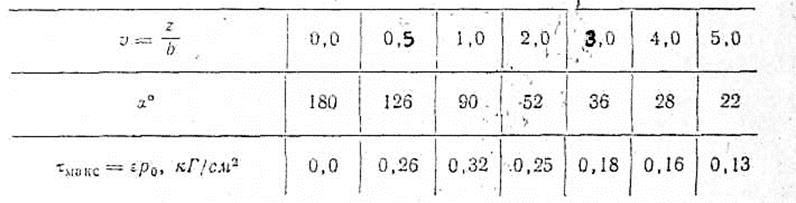
Эпюра распределения τ_макс по оси симметрии фундамента показана на рис. 8.

 

	Рис. 8. Эпюра максимальных касательных напряжений τ макс по глубине по оси симметрии полосообразной нагрузки