Напряжения в грунте. Главные и касательные напряжения в условии плоской задачи

Лекция № 4

НАПРЯЖЕНИЯ В ГРУНТЕ.

ГЛАВНЫЕ И КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ

В УСЛОВИИ ПЛОСКОЙ ЗАДАЧИ

Напряженное состояние в любой точке грунтового массива до возведения сооружения определяется собственным весом перекрывающей толщи грунта; оно возрастает с глубиной.

Дополнительное напряжение, возникающее в основании под воздействием давления от сооружения, наоборот, убывает с глубиной. Это напряженное состояние в основании можетбыть определено либо через главные, либо через касательные и нормальные напряжения.

Условия плоской задачи имеют место в случае распределения напряжений в одной плоскости, в перпендикулярном направлении они будут или равны нулю, или постоянны. Справедливо для очень вытянутых в плане сооружений , например ленточных и стеновых фундаментов, оснований подпорных стенок, насыпей и подобных сооружений.

ГЛАВНЫЕ НАПРЯЖЕНИЯ

Напряженное состояние в любой точке грунтового массива при равномерно распределенной нагрузке р₀, может быть наглядно изображено при помощи эллипса напряжений, построенного на главных напряжениях р₁  и  р₂ как на своих полуосях (рис. 1).    

Главные   напряжения  характеризуют напряженное состояние в заданной точке в целом, вне зависимости от ориентации площадок, проведенных через данную точку. Они являются самым большим и самым меньшим из всех полных напряжений, которые могут действовать по любойиз площадок, проведенных через данную точку.

Величина главных напряжений р₁ и р₂ и направление их действия непрерывно изменяются с изменением места расположения рассматриваемой точки в основании сооружения.

Направление действия большего главного напряжения р₁ совпадает с биссектрисой угла видимости α.

Величина главных напряжений для случая равномерно распределенной  нагрузки определяется зависимостями:

где р₀ — передаваемая на грунт сооружением равномерно распределенная удельная нагрузка, кН /м²;

а — угол   видимости.

Значения главных напряжений р₁ и р₂ можно также определять по графику 1 прил. 1. График построен в относительных координатах υи d:

где υ— условная   ордината   рассматриваемой   точки   грунтового массива;

d— условная   абсцисса   рассматриваемой   точки   грунтового массива;

z— глубина   залегания   рассматриваемой   точки   грунтового массива от подошвы фундамента (рис. 1);

х — расстояние   рассматриваемой   точки   грунтового   массива от оси симметрии фундамента.

Коэффициенты μ и v на кругах напряжений графика отвечают значениям р₁ и р₂ при  р₀ = 1 кН/м³  и, следовательно, значения главных напряжений равны:

р₁ = μ· р₀; (57)

p₂ = v ·p₀,                                   (58)

где         р_о — передаваемая    сооружением    равномерно   распределенная нагрузка на грунт;  μ и v — коэффициенты   пропорциональности.  

Значения коэффициентов пропорциональности μ и v можно также определять по табл. 1 прил. 2.

Пример 1. Поверхность земли нагружена полосообразной равномерно распределенной нагрузкой с интенсивностью р₀ = 2 кН/м². Ширина полосы загрузки 2b= 2 м. Определить величину и направление действия главных напряжений р₁и p₂ в точке А с координатами х = 2 м; z = 4 м.

Решение.

1. По координатам наносим положение точки А (рис. 2).

2. Определяем значение угла видимости αиз двух прямоугольных треугольников: ABDи АСD.

Значение угла α в радианах равно:

3. По формулам (53), (54) определяем значения главных напряжений.

Этиже значения главных напряжений можно получить либо по графику 1 приложения 1, либо по табл. 1 приложения 2.

4. В первом случае значения главных напряжений проще всего определяются через относительные координаты υи d. В условиях примера они равны:

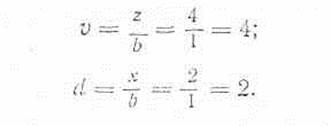
На графике 1 прил. 1 находим положение точки с координатами  υ= 4 и d= 2. Она оказалась между кругов равных напряжений с углами видимости        α = 20° и  25°. По интерполяции находим, что α= 23°.

Точно также по интерполяции находим значения переходных коэффициентов μ и v к формулам (57), (58): для определения главных   напряжений р₁ и р_г: при а₁ = 20^о значения μ = 0,23 и v =  0,00;  при α₂ = 25^о значения μ = 0,27 и v = 0,01.

Следовательно, значения μ и v для а = 23^о следующие:

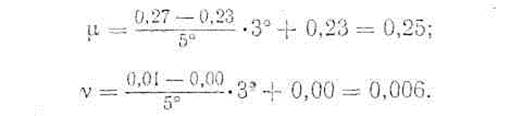
Тогда   согласно формулам (57), (58) получим

р₁ = 0,25·2 = 0,5 кН/м², р₂ = 0,006·2  = 0,01  кН/м².

5. Зная величину угла видимости а по табл. 1 приложения 2, можно определить значения переходных коэффициентов μ и v и по формулам (57), (58) — значения главных напряжений p₁и р₂.

Ход решения совершенно такой же, как ив случае определения главных напряжений по графику 1 приложения  1 (см. п. 4).

6. Направление главных напряжений определяется углом видимости α: большее главное напряжение p₁направлено по биссектрисе угла а, меньшее р₂ — перпендикулярно ему, рис. 2.

 

Рис. 2. Схема к решению примера